გამოკლების გამოთვლის 6 გზა

2024 ავტორი: Jason Gerald | [email protected]. ბოლოს შეცვლილი: 2024-01-19 22:13

გამოკლება არის უბრალოდ ერთი რიცხვის გამოკლება მეორისგან. ადვილია ერთი მთლიანი რიცხვის გამოკლება მეორისგან, მაგრამ გამოკლება შეიძლება სახიფათო იყოს, თუ გამოვაკლებთ წილადებს ან ათწილადებს. მას შემდეგ რაც გაიგებთ გამოკლებას, თქვენ შეძლებთ გამოიყენოთ უფრო რთული მათემატიკური ცნებები და შეძლებთ რიცხვების დამატებას, გამრავლებას და გაყოფას უფრო ადვილად.

ნაბიჯი

მეთოდი 1 – დან 6 – დან: სესხის აღებით დიდი რიცხვების გამოკლება

ნაბიჯი 1. ჩაწერეთ დიდი რიცხვი

მაგალითად, გსურთ ამოხსნათ 32 - 17. ჩაწერეთ პირველი 32.

ნაბიჯი 2. ჩაწერეთ პატარა რიცხვი მის ქვემოთ

დარწმუნდით, რომ ათეულის და ერთის მნიშვნელობები მოათავსეთ სწორ სვეტებში, ისე რომ 32 – დან 3 იყოს პირდაპირ 17 – ის 1 – ზე ზემოთ და 32 – დან 2 – ია პირდაპირ 17 – დან 7 – ზე.

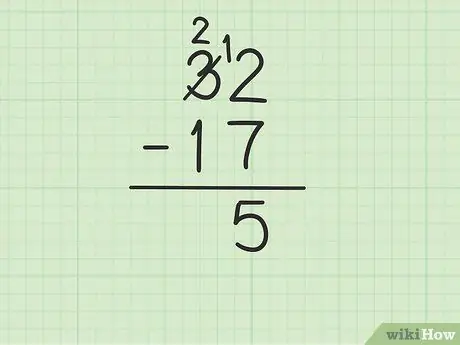
ნაბიჯი 3. გამოაკელით ერთეულების სვეტში ზედა რიცხვი ქვედა რიცხვიდან

თუმცა, ეს შეიძლება გართულდეს, თუ ქვედა რიცხვი უფრო დიდია, ვიდრე ზედა რიცხვი. ამ შემთხვევაში, 7 არის 2 -ზე მეტი. აი რა უნდა გააკეთოთ:

თქვენ უნდა ისესხოთ 32 რიცხვიდან 3 (ასევე ცნობილია როგორც დაჯგუფება), რომ 2 გახდეთ 12 -მდე.
გადაკვეთეთ 32 რიცხვიდან 3 და შეცვალეთ იგი რიცხვით 2, ხოლო რიცხვი 2 ხდება 12.
ახლა თქვენ შეგიძლიათ გამოაკლოთ 12 - 7, რაც უდრის 5. ჩაწერეთ 5 იმ ორი რიცხვის ქვეშ, რომელსაც თქვენ გამოაკლებთ ისე, რომ ისინი იყოს ახალი რიგის ერთეულების სვეტში.

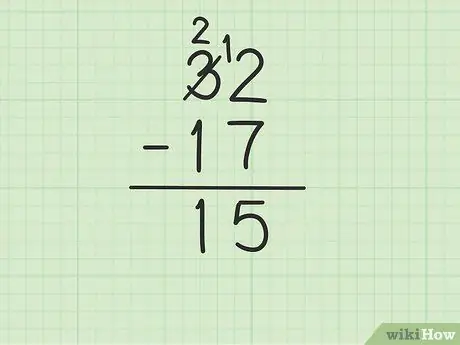
ნაბიჯი 4. ქვედა რიცხვიდან გამოაკელით ათეულის სვეტის ზედა რიცხვი

დაიმახსოვრე 3 გახდა 2. ახლა გამოაკელი 1 – ს 17 – დან 2 – დან, რომ მიიღო (2– 1) 1. ჩაწერე 1 ქვემოთ, ათეულების სვეტში, 5 – ის მარცხნივ, ერთეულების სვეტში. თქვენ წერთ 15. ანუ 32 - 17 = 15.

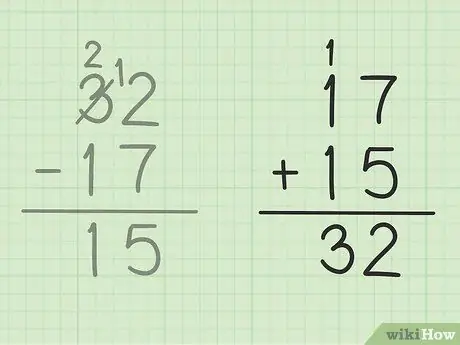
ნაბიჯი 5. შეამოწმეთ თქვენი სამუშაო

თუ გსურთ დარწმუნდეთ, რომ სწორად გამოაკელით ორი რიცხვი, მაშინ ყველაფერი რაც თქვენ უნდა გააკეთოთ არის დაამატოთ თქვენი პასუხი უფრო მცირე რიცხვით, რომ მიიღოთ დიდი რიცხვი. ამ ამოცანაში თქვენ უნდა დაამატოთ თქვენი პასუხი, 15 გამოკლების მცირე რაოდენობას, 17. 15 + 17 = 32, ისე რომ თქვენი პასუხი სწორი იყოს. Უსაფრთხო!

მეთოდი 2 -დან 6 -დან: გამოაკელი მცირე მთლიანი რიცხვები

ნაბიჯი 1. იპოვეთ უფრო დიდი რიცხვი

პრობლემებს, როგორიცაა 15 -9, განსხვავებული გზა ექნება, ვიდრე 2 -30.

15 - 9 კითხვებში პირველი რიცხვი, 15, მეორე რიცხვზე მეტია, 9.
კითხვებზე 2 - 30, მეორე რიცხვი, 30, უფრო დიდია, ვიდრე პირველი რიცხვი, 2.

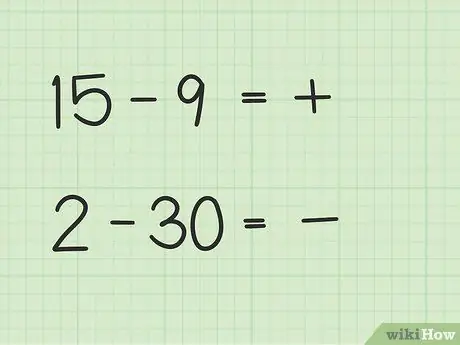
ნაბიჯი 2. გადაწყვიტეთ თქვენი პასუხი იქნება დადებითი ან უარყოფითი

თუ პირველი რიცხვი უფრო დიდია, პასუხი დადებითია. თუ მეორე რიცხვი უფრო დიდია, პასუხი უარყოფითია.

პირველ კითხვაზე, 15 - 9, თქვენი პასუხი დადებითია, რადგან პირველი რიცხვი მეორე რიცხვზე მეტია.
მეორე კითხვაზე, 2 - 30, თქვენი პასუხი უარყოფითია, რადგან მეორე რიცხვი პირველ რიცხვზე მეტია.

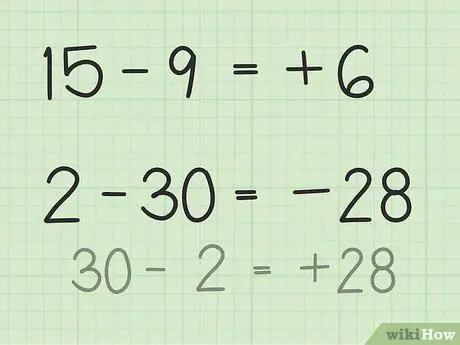
ნაბიჯი 3. იპოვეთ განსხვავება ორ რიცხვს შორის

ორი რიცხვის გამოკლების მიზნით, თქვენ უნდა წარმოიდგინოთ განსხვავება ორ რიცხვს შორის და გამოთვალოთ რიცხვები მათ შორის.

15 - 9 კითხვებისთვის წარმოიდგინეთ 15 პოკერის ჩიპი. გადაყარეთ 9 ჩიპი და მხოლოდ 6. ასე რომ, 15 - 9 = 6. თქვენ ასევე შეგიძლიათ წარმოიდგინოთ რიცხვითი წრფე. დაფიქრდით რიცხვებზე 1 -დან 15 -მდე, შემდეგ გადაყარეთ ან დააბრუნეთ 9 ერთეული, რომ მიიღოთ 6.
კითხვებისთვის 2 - 30, ამის გადაჭრის უმარტივესი გზაა რიცხვის შებრუნება და გამოკლების შემდეგ შედეგი უარყოფითი. ამრიგად, 30 - 2 = 28 ასე რომ 28 და 30 – ს აქვს 2. სხვაობა. ასე რომ, 2 -30 = -28.

მეთოდი 3 -დან 6 -დან: ათწილადების გამოკლება

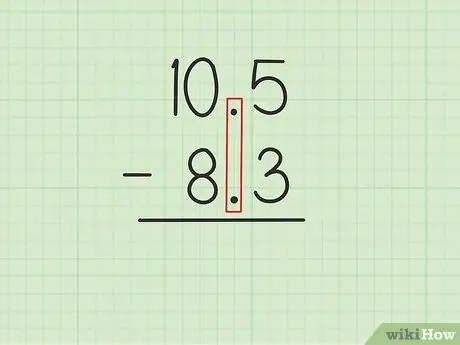
ნაბიჯი 1. ჩაწერეთ უფრო დიდი რიცხვი პატარა რიცხვზე ათწილადების ათვლით

დავუშვათ, რომ გსურთ შემდეგი პრობლემების გადაჭრა: 10, 5 - 8, 3. ჩაწერეთ 10, 5 8 -ზე, 3 -ზე ისე, რომ ორი რიცხვის ათწილადები პარალელური იყოს., 10 -დან 5, 5 უნდა იყოს პირდაპირ ზემოთ, 3 8 -დან, 3 -დან და 10 -დან 0, 5 უნდა იყოს 8 -დან 8 -ზე, 3 -ზე.

თუ თქვენ გაქვთ პრობლემა, რადგან ორ რიცხვს არ აქვს ერთი და იგივე რიცხვი ათწილადის შემდეგ, ჩაწერეთ 0 ცარიელში, სანამ რიცხვების ჯამი არ იქნება იგივე. მაგალითად, პრობლემა არის 5, 32 - 4, 2, შეგიძლიათ ჩაწეროთ როგორც 5, 32 - 4, 2 0 რა ეს არ შეცვლის მეორე რიცხვის მნიშვნელობას, მაგრამ გაადვილებს ორი რიცხვის გამოკლებას.

ნაბიჯი 2. გამოაკელით ათეულების სვეტის ზედა რიცხვი ქვემოთ მოცემული რიცხვიდან

ამ შემთხვევაში, თქვენ უნდა გამოაკლოთ 3 -ს 5 -დან. 5 - 3 = 2, ასე რომ თქვენ უნდა დაწეროთ 2 3 -დან 8, 3.

დარწმუნდით, რომ ჩაწერეთ ათობითი წერტილი პასუხში ისე, რომ დაიწეროს, 2

ნაბიჯი 3. გამოაკელით ერთეულების სვეტის ზემოთ რიცხვი მის ქვემოთ მოცემულ რიცხვს

თქვენ უნდა გამოაკლოთ 8 -დან 0. სესხება 1 ათეულების ნაწილიდან რომ შეიცვალოს 0 -დან 10 -მდე და გამოაკლოთ 10 - 8 რომ მიიღოთ 2. ასევე შეგიძლიათ დაითვალოთ 10 - 8 სესხის აღების გარეშე, რადგან მეორე ათეულების სვეტში არ არის რიცხვები. ჩაწერეთ პასუხი 8 – ის ქვემოთ, ათწილადის მარცხნივ.

ნაბიჯი 4. ჩაწერეთ თქვენი საბოლოო შედეგი

თქვენი საბოლოო შედეგი არის 2, 2.

ნაბიჯი 5. შეამოწმეთ თქვენი სამუშაო

თუ გსურთ დარწმუნდეთ, რომ თქვენი ათწილადის გამოკლება სწორია, თქვენ მხოლოდ უნდა დაამატოთ თქვენი პასუხი უფრო მცირე რიცხვით, რომ გახადოთ უფრო დიდი რიცხვი. 2, 2 + 8, 3 = 10, 5, ასე რომ თქვენ დაასრულეთ.

მეთოდი 4 დან 6: გამოაკელით წილადები

ნაბიჯი 1. წილადის მნიშვნელისა და მრიცხველის გასწორება

დავუშვათ, რომ გსურთ პრობლემების გადაჭრა 13/10 - 3/5. დაწერეთ პრობლემა ისე, რომ ორი მრიცხველი, 13 და 3 და ორი მნიშვნელი, 10 და 5 ერთმანეთის საპირისპიროა. ეს ორი რიცხვი გამოყოფილია გამოკლების ნიშნით. ეს დაგეხმარებათ პრობლემის ვიზუალიზაციაში და უფრო მარტივად გადაჭრაში.

ნაბიჯი 2. იპოვეთ უმცირესი საერთო მნიშვნელი

ყველაზე ნაკლებად საერთო მნიშვნელი არის ყველაზე პატარა რიცხვი, რომელიც შეიძლება გაიყოს ორ რიცხვზე. ამ მაგალითში თქვენ უნდა იპოვოთ ყველაზე პატარა საერთო მნიშვნელი, რომელიც იყოფა 10 -ზე და 5 -ზე. თქვენ ნახავთ, რომ 10 არის ყველაზე პატარა საერთო მნიშვნელი ორივე რიცხვისთვის, რადგან 10 იყოფა 10 -ზე და 5 -ზე.

გაითვალისწინეთ, რომ ორი რიცხვის უმცირესი საერთო მნიშვნელი ყოველთვის არ არის ერთი მათგანი. მაგალითად, 3 და 2 -ის ყველაზე პატარა საერთო მნიშვნელი არის 6, რადგან 6 არის ყველაზე პატარა რიცხვი, რომელიც შეიძლება გაიყოს ორ რიცხვზე

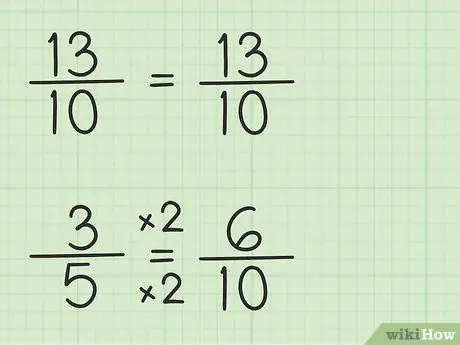
ნაბიჯი 3. დაწერეთ წილადები ერთი და იმავე მნიშვნელის გამოყენებით

წილადი 13/10 შეიძლება დაიწეროს ერთნაირად, რადგანაც მნიშვნელი არის 10, ყველაზე პატარა საერთო მნიშვნელი, რაც არის 10, გამრავლებული 1. თუმცა, წილადი 3/5 უნდა გადაწერილი იყოს, რადგანაც მნიშვნელი არის 5, ყველაზე პატარა საერთო მნიშვნელი, რომელიც არის 10, გამრავლებული 2. ამრიგად, წილადი 3/5 უნდა გამრავლდეს 2/2 - ით, რომ მნიშვნელი იყოს 10, ასე რომ 3/5 x 2/2 = 6/10. თქვენ იპოვეთ ექვივალენტი წილადი. 3/5 ექვივალენტია 6/10, თუმცა 6/10 საშუალებას გაძლევთ გამოაკლოთ პირველი რიცხვი, 13/10.

დაწერე ახალი შეკითხვა ასე: 13/10 - 6/10

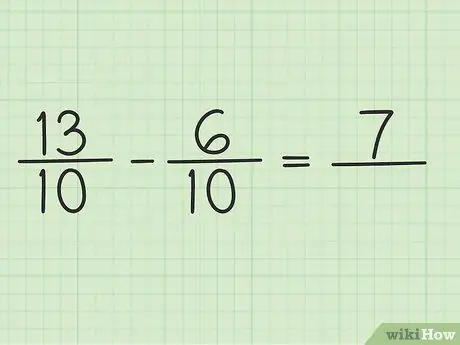
ნაბიჯი 4. მრიცხველი გამოვაკლოთ ორ რიცხვს

უბრალოდ გამოაკელით 13 - 6 ასე რომ შედეგი არის 7. თქვენ არ შეგიძლიათ შეცვალოთ წილადის მნიშვნელი.

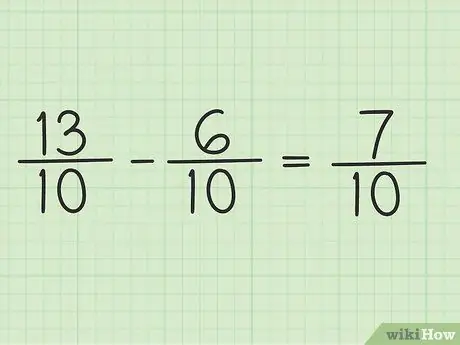
ნაბიჯი 5. ჩაწერეთ ახალი მრიცხველი იმავე მნიშვნელზე, რომ მიიღოთ საბოლოო შედეგი

ახალი მრიცხველი არის 7. ორივე წილადს აქვს მნიშვნელი 10. თქვენი საბოლოო შედეგი არის 7/10.

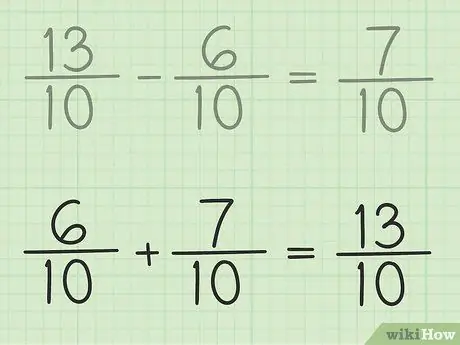
ნაბიჯი 6. შეამოწმეთ თქვენი სამუშაო

თუ გსურთ დარწმუნდეთ, რომ სწორად გამოაკლებთ წილადს, უბრალოდ დაამატეთ თქვენი პასუხი და მცირე წილადი ისე, რომ შედეგი იყოს უფრო დიდი წილადი. 7/10 + 6/10 = 13/10. დამთავრდა.

მეთოდი 5 -დან 6 -დან: წილადების გამოკლება მთელი რიცხვიდან

ნაბიჯი 1. ჩაწერეთ პრობლემა

მაგალითად, დავუშვათ, რომ გსურთ შემდეგი პრობლემის გადაჭრა: 5 -. ჩამოწერეთ.

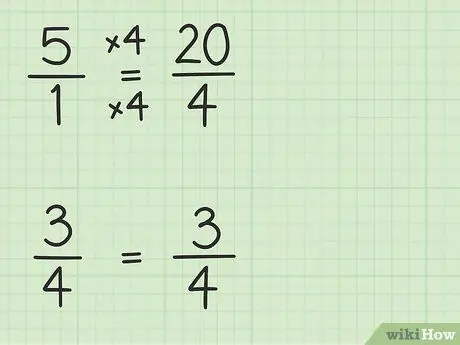
ნაბიჯი 2. გადააკეთეთ მთელი რიცხვები წილადებად, რომლებსაც აქვთ იგივე მნიშვნელი, როგორც სხვა წილადებს

თქვენ გადააქცევთ 5 – ს წილად 4 –ის მნიშვნელით, რომ შეძლოთ ორი რიცხვის გამოკლება. ასე რომ თქვენ უნდა იფიქროთ 5 –ზე, როგორც 5/1 ფრაქცია. შემდეგ, შეგიძლიათ გაამრავლოთ ახალი წილადის მრიცხველი და მნიშვნელი 4 -ით, რათა ორი რიცხვის მნიშვნელი იგივე იყოს. ასე რომ 5/1 x 4/4 = 20/4. ეს წილადი უდრის 5 -ს, მაგრამ გაძლევთ საშუალებას გამოაკლოთ ორი რიცხვი.

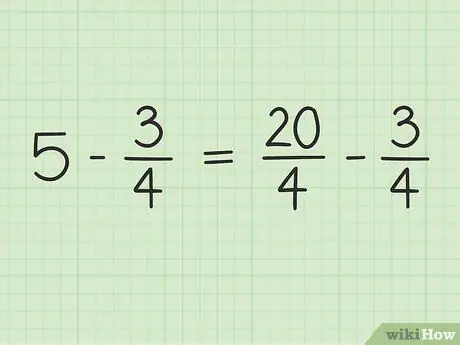
ნაბიჯი 3. გადაწერეთ პრობლემა

ახალი პრობლემა შეიძლება დაიწეროს ასე: 20/4 - 3/4.

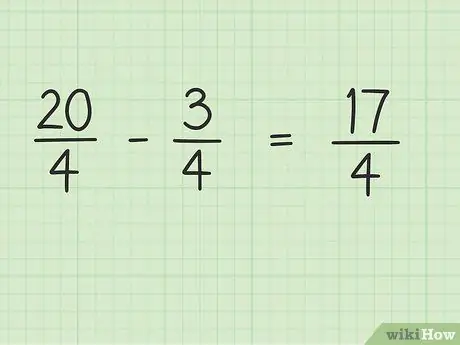
ნაბიჯი 4. გამოვაკლოთ წილადის მრიცხველი, ხოლო მნიშვნელი იგივე რჩება

ახლა, უბრალოდ გამოაკელით 20 -ს 3 -ით, რომ მიიღოთ საბოლოო შედეგი. 20 - 3 = 17, ანუ 17 არის ახალი მრიცხველი. თქვენ შეგიძლიათ დატოვოთ მნიშვნელი იგივე.

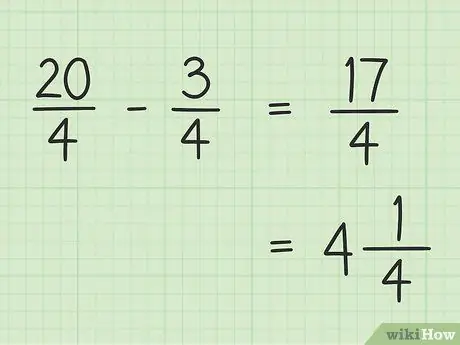
ნაბიჯი 5. ჩაწერეთ თქვენი საბოლოო შედეგი

თქვენი საბოლოო შედეგი არის 17/4. თუ გსურთ შერეული რიცხვის ჩაწერა, გაყავით 17 -ზე 4 -ზე ისე, რომ შედეგი იყოს 4, ხოლო დანარჩენი 1, ისე რომ თქვენი საბოლოო 17/4 უდრის 4 -ს.

მეთოდი 6 -დან 6: ცვლადების გამოკლება

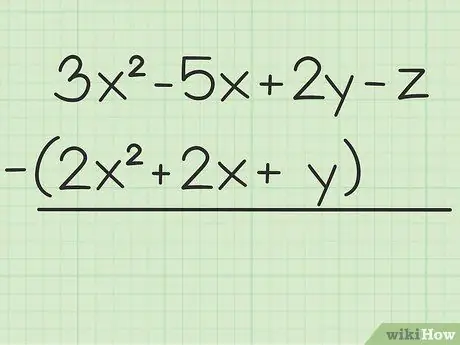
ნაბიჯი 1. ჩამოწერეთ პრობლემა, რომლის გადაწყვეტაც გსურთ

მაგალითად შემდეგი შეკითხვა: 3x² - 5x + 2y - z - (2x² + 2x + y). დაწერეთ ცვლადების პირველი ნაკრები მეორეზე.

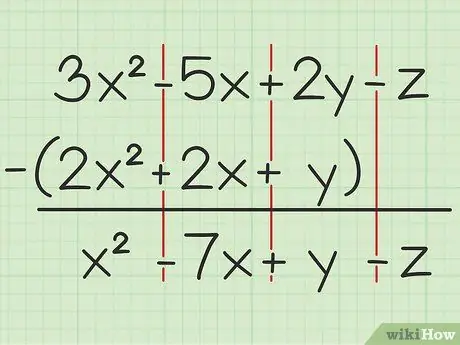
ნაბიჯი 2. ერთი და იგივე ცვლადების გამოკლება

თუ თქვენ შეხვდებით ცვლადს, შეგიძლიათ დაამატოთ ან გამოაკლოთ იგივე ცვლადი და რომელიც დაწერილია კვადრატის იგივე ხარისხით. ეს ნიშნავს, რომ თქვენ შეგიძლიათ გამოაკლოთ 4 ჯერ² 7x– დან², მაგრამ არ შეიძლება გამოაკლოს 4x 4y– დან. ამრიგად, თქვენ შეგიძლიათ გაანალიზოთ პრობლემა შემდეგნაირად:

3x² - 2x² = x²
-5x -2x = -7x
2y - y = y
-z -0 = -z

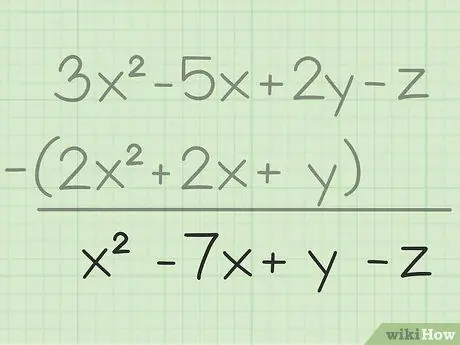
ნაბიჯი 3. ჩაწერეთ თქვენი საბოლოო შედეგი

თქვენ გამოაკლეთ ყველა ერთი და იგივე ცვლადი, ყველაფერი რაც თქვენ უნდა გააკეთოთ არის დაწეროთ თქვენი საბოლოო შედეგი, რომელიც შეიცავს თქვენს მიერ გამოკლებულ ყველა ცვლადს. აქ არის საბოლოო შედეგი: