- ავტორი Jason Gerald [email protected].
- Public 2023-12-16 11:21.
- ბოლოს შეცვლილი 2025-06-01 06:06.
წილადების დამატება ძალიან სასარგებლო ცოდნაა. ამ უნარის სწავლა და გამოყენება ძალიან ადვილია მათემატიკის პრობლემებზე მუშაობის დაწყებიდან დაწყებული დაწყებითი კლასებიდან დაწყებული. ეს სტატია განმარტავს, თუ როგორ უნდა დაამატოთ წილადები, ასე რომ თქვენ შეგიძლიათ ამის გაკეთება სულ რამდენიმე წუთში.
ნაბიჯი
მეთოდი 1 -დან 2: წილადების დამატება ერთი და იგივე მნიშვნელობით

ნაბიჯი 1. შეამოწმეთ თითოეული წილადის მნიშვნელი (რიცხვი კოეფიციენტის ქვეშ)
თუ რიცხვები ერთნაირია, მაშინ თქვენ დაამატებთ წილადებს ერთი და იგივე მნიშვნელობით. თუ მნიშვნელი განსხვავებულია, წაიკითხეთ მეორე მეთოდი.
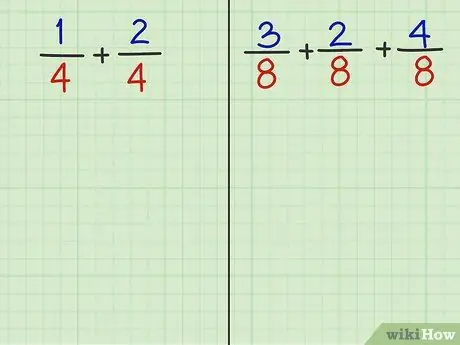
ნაბიჯი 2. უპასუხეთ შემდეგ 2 კითხვას
ამ მეთოდის ბოლო ნაბიჯის წაკითხვით, თქვენ უნდა შეგეძლოთ დაამატოთ შემდეგი ორი კითხვის წილადი.
- პრობლემა 1: 1/4 + 2/4
- პრობლემა 2: 3/8 + 2/8 + 4/8
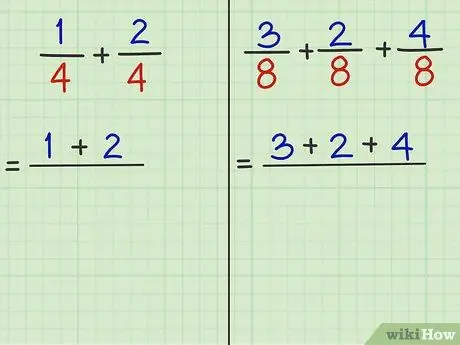
ნაბიჯი 3. შეაგროვეთ მრიცხველები (რიცხვები გაყოფის ზემოთ) და დაამატეთ ისინი
მრიცხველი არის რიცხვი კოეფიციენტის ზემოთ. რამდენი წილადის დამატება გსურთ, შეგიძლიათ დაუყოვნებლივ დაამატოთ მრიცხველები, თუ მნიშვნელი იგივეა.
- პრობლემა 1: 1/4 + 2/4 არის დამატებული წილადი. "1" და "2" არის მრიცხველები. ასე რომ, 1 + 2 = 3.
- პრობლემა 2: 3/8 + 2/8 + 4/8 არის დამატებული წილადი. "3" და "2" და "4" არის მრიცხველები. ასე რომ, 3 + 2 + 4 = 9.

ნაბიჯი 4. განსაზღვრეთ ახალი წილადი ჯამიდან
ჩამოწერეთ მრიცხველი, რომელიც მიღებულია 2. საფეხურზე. ეს რიცხვი არის ახალი მრიცხველი რა დაწერეთ მნიშვნელი, რომელიც ერთი და იგივე რიცხვია თითოეული წილადის ბისექტრის ქვეშ. თქვენ არ გჭირდებათ გამოთვლების გაკეთება, თუ მნიშვნელი იგივეა. ეს რიცხვი არის ახალი მნიშვნელი და ყოველთვის უტოლდება ძველ მნიშვნელს, როდესაც ერთსა და იმავე მნიშვნელის წილადებს დაამატებ.
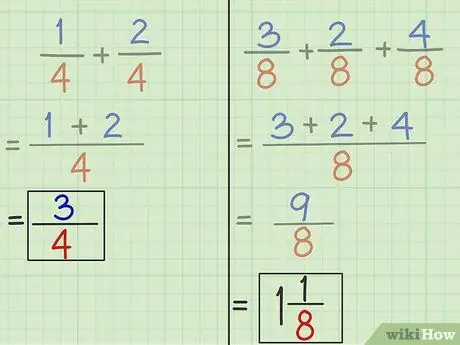
- პრობლემა 1: 3 არის ახალი მრიცხველი და 4 ახალი მნიშვნელი. ამრიგად, 1 კითხვაზე პასუხი არის 3/4. 1/4 + 2/4 = 3/4.
- პრობლემა 2: 9 არის ახალი მრიცხველი და 8 არის ახალი მნიშვნელი. ამრიგად, მე -2 კითხვაზე პასუხი არის 9/8. 3/8 + 2/8 + 4/8 = 9/8.
ნაბიჯი 5. საჭიროების შემთხვევაში გაამარტივეთ წილადები
ნუ დაგავიწყდებათ ახალი წილის გამარტივება, რათა წერა უფრო მარტივი გახდეს.
-
თუ მრიცხველი უფრო დიდი ნაცვლად მნიშვნელისა, როგორიც არის პრობლემა 2 -ის დამატება, ეს ნიშნავს, რომ ჩვენ ვიღებთ 1 მთელ თვეს წილის გამარტივების შემდეგ. გაყავით მრიცხველი მნიშვნელზე ან 9 გაყოფილი 8 - ზე. შედეგი არის მთელი 1 დარჩენილი 1. ჩაწერეთ მთელი რიცხვები წილადის წინ და ნარჩენი ხდება ახალი წილადის მრიცხველი იგივე მნიშვნელით.
9/8 = 1 1/8.
მეთოდი 2 დან 2: წილადების დამატება სხვადასხვა მნიშვნელობით

ნაბიჯი 1. შეამოწმეთ თითოეული წილადის მნიშვნელი (რიცხვი კოეფიციენტის ქვეშ)
თუ მნიშვნელი განსხვავებულია, შენ ხარ დაამატეთ წილადები სხვადასხვა მნიშვნელობით რა წაიკითხეთ შემდეგი ნაბიჯები, რადგან წილადების დამატებამდე მნიშვნელი უნდა გახადოთ თანაბარი.
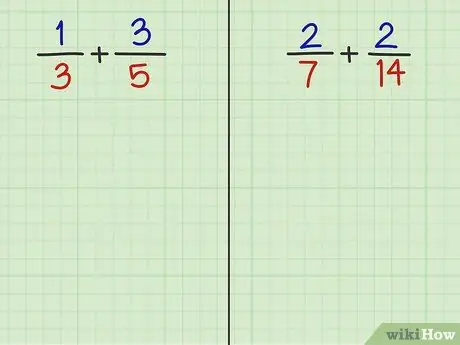
ნაბიჯი 2. ამოხსენით შემდეგი 2 შეკითხვა
ამ მეთოდის ბოლო ნაბიჯის წაკითხვით, თქვენ უნდა შეგეძლოთ დაამატოთ შემდეგი ორი კითხვის წილადი.
- პრობლემა 3: 1/3 + 3/5
- კითხვა 4: 2/7 + 2/14

ნაბიჯი 3. ემთხვევა მნიშვნელს
ამისათვის გაამრავლეთ ორი წილადის მნიშვნელი ზემოთ. მნიშვნელთა გათანაბრების მარტივი გზაა ორი წილადის მნიშვნელის გამრავლება. თუ ერთ -ერთი მნიშვნელი მეორის ჯერადია, იპოვეთ ორი მნიშვნელიდან უმცირესი საერთო ჯერადი.
-
პრობლემა 3:
3 x 5 = 15. ასე რომ, ორივე წილადის ახალი მნიშვნელი არის 15.
-
პრობლემა 4:
14 არის 7 -ის ჯერადი. ამიტომ, ჩვენ მხოლოდ 7 უნდა გავამრავლოთ 2 -ით, რომ მივიღოთ 14. ამრიგად, ორივე წილადის ახალი მნიშვნელი არის 14.

ნაბიჯი 4. გავამრავლოთ პირველი წილადის მრიცხველი და მნიშვნელი მეორე წილადის მნიშვნელზე
ეს ნაბიჯი არ ცვლის წილადის მნიშვნელობას, მაგრამ წილადი იცვლება მნიშვნელის შესატყვისად. წილადი ღირებულება უცვლელი რჩება.
-
პრობლემა 3:
1/3 x 5/5 = 5/15.
-
პრობლემა 4:
ამ პრობლემის გადასაჭრელად, ჩვენ უბრალოდ უნდა გავამრავლოთ პირველი წილადი 2/2 - ით, რომ მნიშვნელი ტოლი იყოს.
2/7 x 2/2 = 4/14

ნაბიჯი 5. გავამრავლოთ მეორე წილადის მრიცხველი და მნიშვნელი პირველი წილის მნიშვნელზე
ზემოთ მოყვანილი ნაბიჯების მსგავსად, ჩვენ არ ვცვლით წილადის მნიშვნელობას, მაგრამ წილადი იცვლება მნიშვნელის გასათანაბრებლად. წილადი ღირებულება უცვლელი რჩება.
-
პრობლემა 3:
3/5 x 3/3 = 9/15.
-
პრობლემა 4:
ჩვენ არ გვჭირდება მეორე წილადის გამრავლება, რადგან მნიშვნელი იგივეა.

ნაბიჯი 6. დაწერეთ ორი ახალი წილადი თანმიმდევრობით
ამ ეტაპზე, ჩვენ არ დავამატეთ ორი წილადი ერთად, თუმცა შეგვიძლია. ზემოაღნიშნულ საფეხურზე ჩვენ გავამრავლებთ თითოეულ წილადს 1. ახლა, ჩვენ გვინდა დავრწმუნდეთ, რომ იმ წილადებს, რომელთა დამატებაც გვინდა, აქვთ ერთი და იგივე მნიშვნელი.
-
პრობლემა 3:
ნაცვლად 1/3 + 3/5, წილადი ხდება 5/15 + 9/15
-
პრობლემა 4:
2/7 + 2/14 ნაცვლად, წილადი ხდება 4/14 + 2/14

ნაბიჯი 7. დაამატეთ ორი წილადის მრიცხველები ერთად
მრიცხველი არის რიცხვი კოეფიციენტის ზემოთ.
-
პრობლემა 3:
5 + 9 = 14. 14 არის ახალი მრიცხველი.
-
პრობლემა 4:
4 + 2 = 6. 6 არის ახალი მრიცხველი.

ნაბიჯი 8. ჩაწერეთ საერთო მნიშვნელი (ნაბიჯი 2) ახალი მრიცხველის ქვეშ ან გამოიყენეთ წილადის მნიშვნელი გამრავლებული 1 -ით მნიშვნელის გასათანაბრებლად
-
პრობლემა 3:
15 არის ახალი მნიშვნელი.
-
პრობლემა 4:
14 არის ახალი მნიშვნელი.

ნაბიჯი 9. დაწერეთ ახალი მრიცხველი და ახალი მნიშვნელი
-
პრობლემა 3:
14/15 არის პასუხი 1/3 + 3/5 =?
-
პრობლემა 4:
6/14 არის პასუხი 2/7 + 2/14 =?

ნაბიჯი 10. წილადების გამარტივება და შემცირება
წილადების გასამარტივებლად მრიცხველი და მნიშვნელი გაყავით ორი რიცხვის უდიდესი საერთო ფაქტორით.
-
პრობლემა 3:
14/15 არ შეიძლება გამარტივდეს.
-
პრობლემა 4:
6/14 შეიძლება შემცირდეს 3/7 მრიცხველისა და მნიშვნელის გაყოფის შემდეგ, როგორც 6 და 14 - ის უდიდესი საერთო ფაქტორი.
Რჩევები
- წილადების დამატებამდე დარწმუნდით, რომ მნიშვნელი იგივეა.
- ნუ დაამატებთ მნიშვნელს. თუ მნიშვნელი ერთნაირია, გამოიყენეთ რიცხვი მნიშვნელად წილადების დამატების შემდეგ.
- თუ გსურთ დაამატოთ წილადები რიცხვებით, რომლებიც შედგება მთლიანი რიცხვებისა და წილადებისაგან, გადააკეთეთ ეს რიცხვები წილადებად და დაამატეთ ისინი ზემოთ მოცემული ინსტრუქციის შესაბამისად.






