სტატისტიკაში დიაპაზონი არის განსხვავება მონაცემთა ნაკრების ყველაზე მაღალ მნიშვნელობასა და მონაცემთა ნაკრების ყველაზე დაბალ მნიშვნელობას შორის. დიაპაზონი აჩვენებს რამდენად გავრცელებულია მნიშვნელობები სერიაში. თუ დიაპაზონი დიდი რიცხვია, მაშინ სერიის მნიშვნელობები ძალიან გაფანტულია; თუ დიაპაზონი მცირე რიცხვია, მაშინ სერიის მნიშვნელობები ერთმანეთთან ახლოს არის. თუ გსურთ იცოდეთ როგორ გამოვთვალოთ მიღწევა, უბრალოდ მიყევით ამ ნაბიჯებს.
ნაბიჯი
ნაბიჯი 1. ჩამოთვალეთ თქვენი მონაცემთა ნაკრების ელემენტები
მონაცემთა ნაკრების დიაპაზონის საპოვნელად, თქვენ უნდა ჩამოთვალოთ მონაცემთა ნაკრების ყველა ელემენტი, რათა შეძლოთ ყველაზე დიდი და უმცირესი რიცხვების ამოცნობა. ჩამოწერეთ ყველა ელემენტი. ამ მონაცემთა ნაკრების რიცხვებია: 14, 19, 20, 24, 25 და 28.
- უფრო ადვილია მონაცემთა ნაკრებში ყველაზე დიდი და უმცირესი რიცხვების ამოცნობა, თუ შეუკვეთებთ რიცხვებს უმცირესიდან ყველაზე დიდამდე. ამ მაგალითში, მონაცემთა ნაკრები ასე იქნება სტრუქტურირებული: 14, 19, 20, 24, 24, 25, 28.
- მონაცემთა ნაკრების ელემენტების დახარისხება ასევე დაგეხმარებათ სხვა გამოთვლების შესრულებაში, როგორიცაა მონაცემთა ნაკრების რეჟიმის, საშუალო ან მედიანის პოვნა.
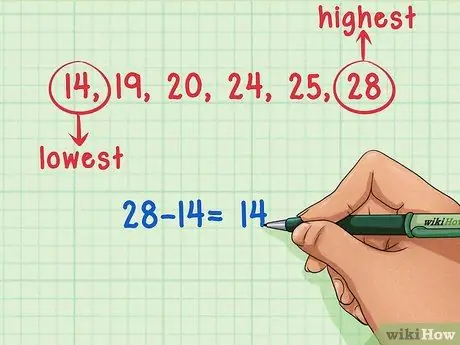
ნაბიჯი 2. განსაზღვრეთ მონაცემთა ნაკრებში ყველაზე დიდი და პატარა რიცხვები
ამ პრობლემისას, მონაცემთა ნაკრებში ყველაზე მცირე რიცხვია 14 და ყველაზე დიდი რიცხვი 28.
ნაბიჯი 3. გამოაკელით ყველაზე მცირე რიცხვი თქვენს მონაცემთა ნაკრებში ყველაზე დიდი რიცხვიდან
ახლა, როდესაც თქვენ განსაზღვრეთ მონაცემთა ნაკრებში ყველაზე პატარა და უდიდესი რიცხვები, ყველაფერი რაც თქვენ უნდა გააკეთოთ არის მათი ერთმანეთისგან გამოკლება. გამოაკელით 14 25 -დან (25 - 14), რომ მიიღოთ 11, მონაცემთა ნაკრების დიაპაზონი.
ნაბიჯი 4. მკაფიოდ მონიშნეთ დიაპაზონი
მას შემდეგ რაც იპოვით დიაპაზონს, მკაფიოდ მონიშნეთ იგი. ეს დაგეხმარებათ თავიდან აიცილოთ დაბნეულობა სხვა სტატისტიკურ გამოთვლებთან, რომლებიც შეიძლება დაგჭირდეთ, როგორიცაა მედიანის, რეჟიმის ან საშუალო მნიშვნელობის პოვნა.
Რჩევები
- თქვენ ასევე შეგიძლიათ ალტერნატიული თვალსაზრისით დიაპაზონის ინტერპრეტაცია, მაგრამ ჯერ უნდა გესმოდეთ ალგებრული ფუნქციის კონცეფცია, ან ცნობილი რიცხვების ოპერაციების ერთობლიობა. იმის გამო, რომ ფუნქციური ოპერაციები შეიძლება შესრულდეს ნებისმიერ რიცხვზე, თუნდაც უცნობ რიცხვზე, რიცხვი აღინიშნება ასო ცვლადით, ჩვეულებრივ x. დომენი არის შესაძლო შეყვანის მნიშვნელობების ერთობლიობა, რომლის შეცვლა შეგიძლიათ უცნობი რიცხვით. ამრიგად, დიაპაზონი არის გამოთვლის შესაძლო შედეგების ერთობლიობა, რომელსაც თქვენ მიიღებთ დომენის ერთ – ერთი მნიშვნელობის შეყვანის და ფუნქციით განსაზღვრული ყველა ოპერაციის დასრულების შემდეგ. სამწუხაროდ, არ არსებობს საშუალება გამოვთვალოთ ფუნქციის დიაპაზონი. ზოგჯერ, ფუნქციის გრაფიკზე გამოსახვა ან მრავალჯერადი მნიშვნელობების გამოთვლა შეიძლება აჩვენოს ნათელი ნიმუში. თქვენ ასევე შეგიძლიათ გამოიყენოთ თქვენი ცოდნა ფუნქციის დომენის შესახებ, რომ გამოტოვოთ შესაძლო გამომავალი (გამოთვლის შედეგები) მნიშვნელობები, ან შეამციროთ მონაცემთა ნაკრები, რომელიც წარმოადგენს დიაპაზონს.
- ნებისმიერი სტატისტიკური მონაცემების ერთეულის საშუალო ღირებულება წარმოადგენს მონაცემთა ნაკრების საშუალო მნიშვნელობას მონაცემთა განაწილების თვალსაზრისით და არა დიაპაზონით. ასე რომ, თქვენ შეიძლება გინდათ ვივარაუდოთ, რომ მოცემული მონაცემთა ნაკრების მედიანა არის დიაპაზონი 2 -ზე გაყოფილი - ან დიაპაზონის დიაპაზონის ნახევარი - ეს ჩვეულებრივ სიმართლეს არ შეესაბამება. სწორი მედიანის მოსაძებნად, თქვენ უნდა დაალაგოთ მონაცემთა ელემენტები, შემდეგ მოძებნოთ ელემენტი სიის შუაში. ეს ელემენტი არის მედიანა. მაგალითად, თუ თქვენ გაქვთ 29 ელემენტის სია, მე -15 ელემენტს აქვს იგივე დიაპაზონი სიის დასაწყისიდან და სიის ბოლოს, ასე რომ მე -15 ელემენტი არის მედიანა, მიუხედავად იმისა, თუ როგორ უკავშირდება ამ ელემენტის მნიშვნელობა დიაპაზონი
