- ავტორი Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:18.
- ბოლოს შეცვლილი 2025-06-01 06:06.
გაყოფის სხვადასხვა გზა არსებობს. თქვენ შეგიძლიათ გაყოთ ათწილადები, წილადები, ან თუნდაც ექსპონენტები და გამოიყენოთ გრძელი ან მოკლე გაყოფა. თუ გსურთ იცოდეთ რიცხვების გაყოფის სხვადასხვა ხერხი, მიჰყევით ქვემოთ მოცემულ ნაბიჯებს.
ნაბიჯი
მეთოდი 1 5 -დან: გრძელი სერიის განყოფილების შესრულება

ნაბიჯი 1. ჩამოწერეთ კითხვები
ხანგრძლივი გაყოფის მიზნით, მოათავსეთ მნიშვნელი (რიცხვი, რომელიც გაიყოფა) გამყოფი ზოლის გარეთ, ხოლო მრიცხველი (რიცხვი, რომელიც უნდა გაიყოს) გამყოფის ზოლში.
მაგალითად: 136 ÷ 3

ნაბიჯი 2. მრიცხველის პირველი ციფრი გავყოთ მნიშვნელზე (თუ შესაძლებელია)
ამ მაგალითში 1 არ იყოფა 3 -ზე, ასე რომ 0 დაყავით გამყოფი ზოლის ზემოთ და გადადით შემდეგ საფეხურზე. გამოაკელი 1 -ს 0 -ით და ჩაწერე შედეგი ნომრის ქვეშ.

ნაბიჯი 3. მრიცხველის პირველი ციფრის ნარჩენისა და მრიცხველის მეორე ციფრის გაყოფა მნიშვნელზე
ვინაიდან 1 არ შეიძლება იყოფა 3 -ზე, რიცხვი 1 კვლავ გამოიყენება. თქვენ უნდა გამოაკლოთ 3. ახლა, გაყავით 13 - ზე 3. მას შემდეგ, რაც 3 x 4 = 12, განათავსეთ 4 გამყოფი ზოლის ზემოთ (0 - ის მარჯვნივ), შემდეგ გამოაკელით 13 - ს 12 - ზე და ჩაწერეთ შედეგი ქვემოთ.

ნაბიჯი 4. დარჩენილი რიცხვები გავყოთ მნიშვნელად
შეამცირეთ 6 რიცხვი 1 - ის მარჯვნივ, მიიღეთ 16. ახლა, გაყავით 16 - ზე 3. ვინაიდან 3 x 5 = 15, ჩაწერეთ რიცხვი 5 რიცხვის 4 - ის მარჯვნივ და გამოაკელით 16 - ს 15 - ზე და ჩაწერეთ შედეგი (16-15 = 1) მის ქვემოთ.

ნაბიჯი 5. ჩაწერეთ დანარჩენი კოეფიციენტის გვერდით
თქვენი საბოლოო პასუხი არის 45 დარჩენილი 1 ან 45 R1.
მეთოდი 2 5 -დან: მოკლე განყოფილებების შესრულება

ნაბიჯი 1. ჩამოწერეთ კითხვები
ჩაწერეთ მნიშვნელი (რიცხვი, რომელიც უნდა გაიყოს) გამყოფი ზოლის მიღმა, ხოლო მრიცხველი (რიცხვი, რომელიც უნდა გაიყოს) გამყოფი ზოლის შიგნით. გაითვალისწინეთ, რომ მოკლე გაყოფისას მნიშვნელი არ შეიძლება იყოს ერთზე მეტი ციფრი.
მაგალითად, 518 4

ნაბიჯი 2. მრიცხველის პირველი ციფრი გავყოთ მნიშვნელზე
5 4 = 1 R1. მოათავსეთ კოეფიციენტი (1) გრძელი გამყოფი ზოლის ზემოთ. ჩაწერეთ დანარჩენი მრიცხველის პირველი ციფრის ზემოთ. მოათავსეთ პატარა 1 5 -ზე, რომ შეგახსენოთ, რომ თქვენ გაქვთ 1 დარჩენილი 5 -ის გაყოფაზე 4 -ზე. 518 ახლა ასე უნდა გამოიყურებოდეს: 5118

ნაბიჯი 3. გაყავით ნარჩენიდან წარმოქმნილი რიცხვი და მრიცხველის მეორე ციფრი მნიშვნელზე
შემდეგი რიცხვია 11, რომელიც მიიღება ნარჩენი მნიშვნელობიდან (1) და მრიცხველის მეორე ციფრიდან (1). 11 4 = 2 R 3 რადგან 4 x 2 = 8 ნარჩენით 3. ჩაწერეთ ნარჩენი მნიშვნელობა მრიცხველის მეორე ციფრის ზემოთ. განათავსეთ 3 -ზე 1. საწყისი მრიცხველი (518) ახლა ასე გამოიყურება: 51138

ნაბიჯი 4. დარჩენილი რიცხვები გავყოთ მნიშვნელად
დარჩენილი რიცხვი არის 38; რიცხვი 3 მოდის წინა ეტაპის დარჩენილი ნაწილიდან, ხოლო 8 არის მრიცხველის ბოლო ციფრი. გამოთვალე 38 4 = 9 R2. მას შემდეგ, რაც 4 x 9 = 36, დაწერეთ "R2" გამყოფი ზოლის ზემოთ, რადგან 38 - 36 = 2.

ნაბიჯი 5. ჩაწერეთ საბოლოო პასუხი
საბოლოო შედეგი და კოეფიციენტი არის გამყოფი ზოლის ზემოთ. პასუხი არის 518 4 = 129 R2.
მეთოდი 5 -დან 5: გაყავით წილადები

ნაბიჯი 1. ჩამოწერეთ კითხვები
წილადის გაყოფისთვის, უბრალოდ ჩაწერეთ პირველი წილადი, რასაც მოჰყვება გაყოფის სიმბოლო და შემდეგ მეორე წილადი.
მაგალითად: 3/4 5/8

ნაბიჯი 2. გადაუხვიეთ მეორე წილადის მრიცხველს და მნიშვნელს
მეორე ფრაქცია ახლა ორმხრივია.
მაგალითი: 3/4 8/5

ნაბიჯი 3. შეცვალეთ გაყოფის სიმბოლო დროის სიმბოლოზე
წილადის გასაყოფად, თქვენ ამრავლებთ პირველ წილადს მეორის საპასუხოდ.
მაგალითი: 3/4 x 8/5
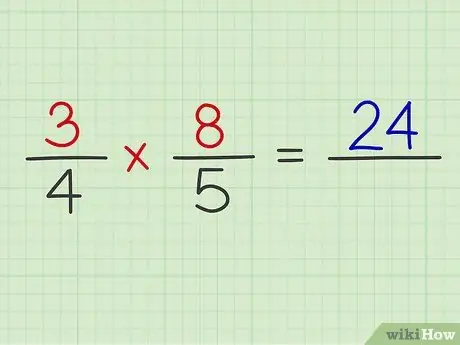
ნაბიჯი 4. გავამრავლოთ ორივე წილადის მრიცხველი
უბრალოდ გააკეთე ეს ისე, როგორც ორი რეგულარული წილადის გამრავლება.
მაგალითი: 3 x 8 = 24
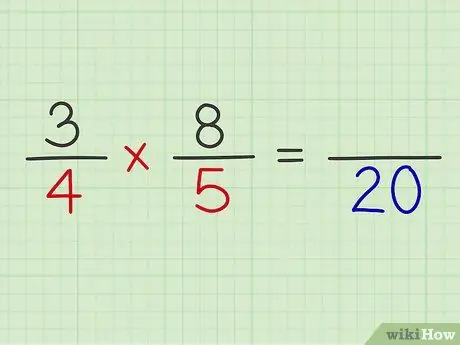
ნაბიჯი 5. გავამრავლოთ ორივე წილადის მნიშვნელი
დაასრულეთ გამოთვლა ორი წილადის გამრავლებით.
მაგალითი: 4 x 5 = 20
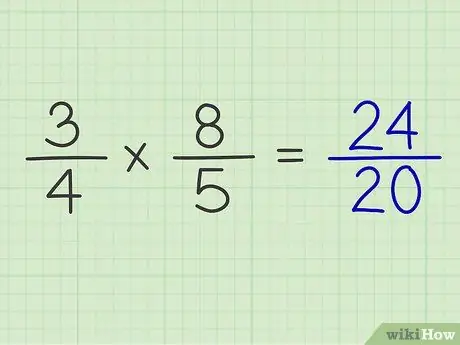
ნაბიჯი 6. დადეთ მრიცხველის პროდუქტი მნიშვნელის პროდუქტზე
ორი წილადის მრიცხველისა და მნიშვნელის გამრავლების შემდეგ შეგიძლიათ მიიღოთ ორივე წილადის გამოთვლის შედეგი.
მაგალითი: 3/4 x 8/5 = 24/20

ნაბიჯი 7. გაამარტივეთ წილადები
უდიდესი საერთო ფაქტორის ან ყველაზე დიდი რიცხვის პოვნა, რომელიც მრიცხველსა და მნიშვნელს თანაბრად ყოფს. ამ შემთხვევაში, 24 -ისა და 20 -ის ყველაზე დიდი საერთო ფაქტორი არის 4. ამის დასამტკიცებლად ჩაწერეთ ყველა მრიცხველი და მნიშვნელი და შემოხაზეთ ორივეს უდიდესი საერთო ფაქტორების რიცხვი.
- 24: 1, 2, 3, 4, 6, 8, 12, 24
-
20: 1, 2, 4, 5, 10, 20
- ვინაიდან 4 არის 24 და 20 - ის უდიდესი საერთო ფაქტორი, უბრალოდ გაყავით ორი რიცხვი 4 -ზე, რათა გაამარტივოთ წილადი.
- 24/4 = 6
- 20/4 = 5
- 24/20 = 6/5

ნაბიჯი 8. გადაწერე წილადი შერეული რიცხვის სახით (სურვილისამებრ)
ხრიკი, უბრალოდ გაყავით მრიცხველი მნიშვნელზე და ჩაწერეთ შედეგი მთლიანი რიცხვით. ამის შემდეგ დაწერეთ გაყოფის დარჩენილი ნაწილი ახალი მრიცხველის სახით და წილადის მნიშვნელი არ იცვლება. მას შემდეგ, რაც 6 გაყოფილი 5 - ზე გამოდის 1 - ში, დარჩენილი 1 - ით, ჩაწერეთ მთელი რიცხვი 1, რასაც მოყვება ახალი მრიცხველი 1, შემდეგ მნიშვნელი 5, რომ მიიღოთ შერეული რიცხვი 1 1/5.
მაგალითი: 6/5 = 1 1/5
მეთოდი 5 -დან 5: გაყავით ექსპონენტი

ნაბიჯი 1. დარწმუნდით, რომ ექსპონენტებს/ძალებს აქვთ იგივე საბაზისო ნომერი
თქვენ შეგიძლიათ გაყოთ ექსპონენტები მხოლოდ იმ შემთხვევაში, თუ მათ აქვთ იგივე საბაზისო ნომერი. წინააღმდეგ შემთხვევაში, შეგიძლიათ სცადოთ მათი მანიპულირება მანამ, სანამ არ მიიღებთ იმავე საბაზისო ნომერს.
მაგალითი: x8 x5

ნაბიჯი 2. გამოვაკლოთ ექსპონენტი
თქვენ შეგიძლიათ უბრალოდ გამოაკლოთ პირველი მაჩვენებელი მეორეს. ნუ გაწუხებთ საბაზისო ნომრები ახლა.
მაგალითი: 8 - 5 = 3
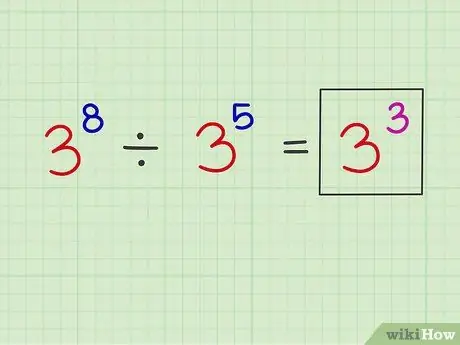
ნაბიჯი 3. განათავსეთ ახალი ექსპონენტი ორიგინალური ძირითადი ნომრის ზემოთ
ახლა თქვენ შეგიძლიათ ჩაწეროთ ახალი გამომცემელი პირვანდელ საბაზო ნომერზე.
მაგალითი: x8 x5 = x3
მეთოდი 5 -დან 5 -დან: ათწილადი რიცხვების გაყოფა

ნაბიჯი 1. ჩამოწერეთ კითხვები
ჩაწერეთ მნიშვნელი (რიცხვი, რომელიც უნდა გაიყოს) გამყოფი ზოლის მიღმა, ხოლო მრიცხველი (რიცხვი, რომელიც უნდა გაიყოს) გამყოფი ზოლის შიგნით. ათობითი გაყოფისას, თქვენი მიზანია ათწილადის რიცხვის მთლიანი რიცხვის გადაყვანა.
მაგალითი: 65.5.5

ნაბიჯი 2. შეცვალეთ მნიშვნელი მთელ რიცხვზე
უბრალოდ გადაიტანეთ ათობითი წერტილი ერთი ციფრით მარჯვნივ, რომ შეცვალოთ 0.5 -დან 5 -მდე, ანუ 5, 0.

ნაბიჯი 3. შეცვალეთ მრიცხველი ათწილადის წერტილის გადაადგილებით იგივე რიცხვით, რაც მნიშვნელი
იმის გამო, რომ მრიცხველის ათწილადს გადააქვთ ერთი ციფრი მარჯვნივ ისე, რომ ის მთლიანი რიცხვი გახდება, მნიშვნელის ათწილადიც გადაინაცვლებს ერთ ციფრს მარჯვნივ ისე, რომ 65.5 იცვლება 655 -ით.
თუ მრიცხველის ათწილადს გადააცილებთ მის ყველა ციფრს, ეს ნიშნავს, რომ თქვენ უნდა დაამატოთ ნულები ციფრებს ყოველ ჯერზე, როდესაც ათწილადი გადავა. მაგალითად, თუ ათობითი წერტილი 7, 2 გადაინაცვლებს სამ ციფრს მარჯვნივ, რიცხვი იცვლება 7,200-მდე, რადგან ორნიშნა ცარიელი სივრცე ივსება ნულებით

ნაბიჯი 4. განათავსეთ ათობითი წერტილი გრძელი გაყოფის ზოლზე მრიცხველის ათწილადის ზემოთ
ვინაიდან თქვენ ათწილადი ერთ ციფრზე გადააქვთ 0.5 მთლიანი რიცხვის შესაქმნელად, კარგი იდეაა, რომ ათწილადის წერტილი განათავსოთ გაყოფის ზოლის ზემოთ ზუსტად იქ, სადაც ათწილადი გადაინაცვლებს, ანუ 655 წლის ბოლო ხუთის შემდეგ.

ნაბიჯი 5. პრობლემის გადაჭრა მარტივი გრძელი გაყოფით
655 -ის 5 -ზე გაყოფისთვის, ნაბიჯებია:
- გაყავით მრიცხველის (6) ასობით ციფრი მნიშვნელზე (5). შედეგი არის 1 ნარჩენებით 1. ჩაწერეთ რიცხვი 1 გამყოფის ზოლზე ზემოთ და ჩაწერეთ 5 გამოსაკლებელი 6 რიცხვის ქვეშ.
- 1 -ის დარჩენილი ნაწილი გამოაკლდება მრიცხველის (5) ათეულების ციფრს, ასე რომ თქვენ ახლა მიიღებთ 15. გაყავით 15 -ზე 5 -ზე და მიიღეთ 3. ჩაწერეთ 3 გამყოფი ზოლის ზემოთ, 1 -ის მარჯვნივ.
- ჩაწერეთ ბოლო 5 ციფრი. გაყავით 5 -ზე 5 -ით, რომ მიიღოთ 1. ჩაწერეთ რიცხვი 1 გამყოფი ზოლის ზემოთ, რიცხვის მარჯვნივ 3. არ არის დარჩენილი, რადგან 5 იყოფა 5 -ზე.
- გრძელი თანმიმდევრული გაყოფის პასუხი არის 655 5 = 131. ეს შედეგი იგივეა, რაც 65.5 0.5.






