საპასუხო ან საპასუხო ძალიან სასარგებლოა ყველა სახის ალგებრული განტოლებისას. მაგალითად, როდესაც თქვენ გაყოფთ ერთ წილადს მეორეზე, თქვენ ამრავლებთ პირველ წილადს მეორის საპასუხოდ. თქვენ ასევე უნდა გამოიყენოთ შებრუნებული, როდესაც ეძებთ ხაზის განტოლებას.
ნაბიჯი
მეთოდი 1 -დან 3: წილადის ან მთლიანი რიცხვის შებრუნებული პოვნა
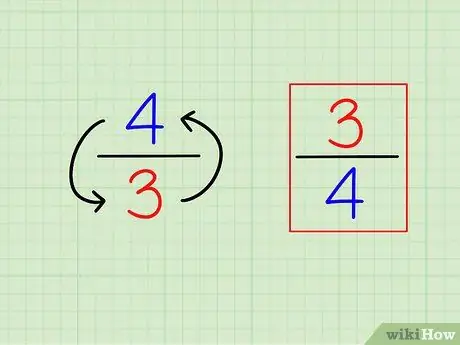
ნაბიჯი 1. იპოვეთ წილადის უკუკავშირი მისი გადაბრუნებით
"საპასუხო" ან საპირისპირო განმარტება ძალიან ადვილია. ნებისმიერი მთლიანი რიცხვის საპასუხოდ, უბრალოდ გამოთვალეთ "1 (ეს რიცხვი)". წილადებისთვის, საპასუხო არის განსხვავებული წილადი, ანუ რიცხვები "გადაბრუნებულია" (შებრუნებული).
- მაგალითად, პირიქით 3/4 არის 4/3.
- ნებისმიერი რიცხვი გამრავლებული მის საპასუხო ბრუნდება 1.
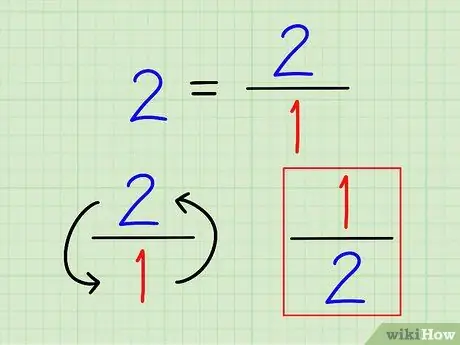
ნაბიჯი 2. ჩაწერეთ მთელი რიცხვის საპასუხო ნაწილი წილად
ისევ და ისევ, რიცხვის საპასუხოა ყოველთვის 1 (ეს რიცხვი). მთელი რიცხვებისთვის ჩაწერეთ ისინი წილადების სახით. აზრი არ აქვს ამ რიცხვის ათწილად გამოთვლას.
მაგალითად, 2 -ის საპასუხო არის 1 2 = 1/2.
3 მეთოდი 2: შერეული წილადის შებრუნებული პოვნა
ნაბიჯი 1. შერეული რიცხვების ამოცნობა
შერეული წილადები შედგება მთელი რიცხვებისა და წილადებისგან, მაგალითად 24/5რა შერეული რიცხვის საპასუხო პოვნის ორი ნაბიჯი არსებობს ქვემოთ აღწერილი.
ნაბიჯი 2. შერეული რიცხვები გადააკეთეთ არასათანადო წილადებად
დაიმახსოვრე, რომ 1 ყოველთვის შეიძლება დაიწეროს როგორც (რიცხვი)/(იგივე რიცხვი), ხოლო ერთნაირი მნიშვნელის მქონე წილადები (ქვედა რიცხვი) შეიძლება დაემატოს ერთად. აქ არის მაგალითი 2 -ის გამოყენებით4/5:
- 24/5
- = 1 + 1 + 4/5
- = 5/5 + 5/5 + 4/5
- = (5+5+4)/5
- = 14/5.
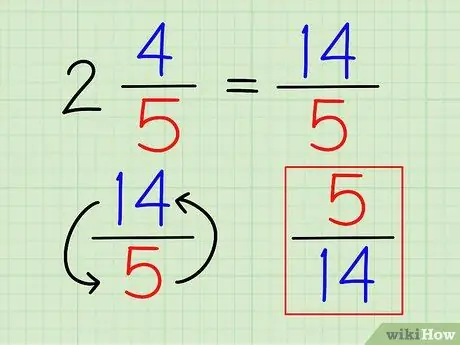
ნაბიჯი 3. გადაატრიალეთ წილადი
მას შემდეგ, რაც რიცხვი დაიწერება მთლიანად როგორც წილადი, თქვენ შეგიძლიათ იპოვოთ მისი საპასუხო ისევე, როგორც სხვა წილადი, წილადის უკუქცევით.
ზემოთ მოყვანილ მაგალითში, საპასუხო 14/5 არის 5/14.
მეთოდი 3 -დან 3: ათწილადის საპირისპირო პოვნა
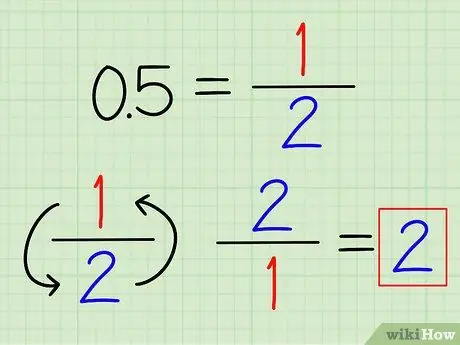
ნაბიჯი 1. გადააკეთეთ ათწილადები წილადებად, თუ ეს შესაძლებელია
თქვენ შეიძლება ამოიცნოთ ხშირად გამოყენებული ათწილადი რიცხვები, რომლებიც ადვილად შეიძლება გადაკეთდეს წილადებად. მაგალითად, 0.5 = 1/2 და 0.25 = 1/4რა მას შემდეგ, რაც ათწილადი გარდაიქმნება წილადზე, უბრალოდ გადაატრიალეთ ეს წილადი, რომ იპოვოთ მისი საპასუხო.
მაგალითად, 0.5 არის საპასუხო 2/1 = 2.
ნაბიჯი 2. დაწერეთ გაყოფის პრობლემა
თუ მას ვერ გადააკეთებთ წილად, გამოთვალეთ რიცხვის საპასუხოდ გაყოფის ამოცანის სახით: 1 (ათობითი). თქვენ შეგიძლიათ გამოიყენოთ კალკულატორი მისი გადასაჭრელად ან გააგრძელოთ შემდეგი ნაბიჯი მისი ხელით გადაჭრისთვის.
მაგალითად, თქვენ შეგიძლიათ ნახოთ 0.4 საპასუხოდ 1 0.4 გამოთვლით
ნაბიჯი 3. შეცვალეთ გაყოფის ამოცანა მთელი რიცხვების გამოსაყენებლად
ათწილადების გაყოფის პირველი ნაბიჯი არის ათწილადის გადატანა მანამ, სანამ ყველა რიცხვი არ იქნება მთლიანი რიცხვი. სანამ ორივე რიცხვის ათწილადს ერთსა და იმავე საფეხურზე გადააქვთ, თქვენ მიიღებთ სწორ პასუხს.
მაგალითად, შეგიძლიათ გამოიყენოთ 1 0, 4 და გადაწეროთ როგორც 10 4. ამ შემთხვევაში, თქვენ გადაინაცვლებთ ყველა ათობითი ადგილს ერთი ნაბიჯით მარჯვნივ, ისევე როგორც ამრავლებთ თითოეულ რიცხვს ათზე
ნაბიჯი 4. პრობლემის გადაჭრა ხანგრძლივი გაყოფის გამოყენებით
გამოიყენეთ გრძელი გაყოფის მეთოდი საპასუხო. თუ დაითვლით 10 4 -ს, მიიღებთ პასუხს 2, 5 რომელიც არის საპასუხო 0, 4.
Რჩევები
- რიცხვის უარყოფითი საპასუხო იგივეა, რაც ჩვეულებრივი საპასუხო, რადგან ის მრავლდება უარყოფითზე. მაგალითად, უარყოფითი საპასუხო 3/4 არის -4/3.
- საპასუხო ან საპასუხო ხშირად მოიხსენიება, როგორც "შებრუნებული გამრავლება".
- რიცხვი 1 თავისთავად საპირისპიროა, რადგან 1 1 = 1.
- 0 რიცხვს არ აქვს ორმხრივი, რადგან 0 განუსაზღვრელია.
