წილადების გაყოფა მთლიანი რიცხვებით არ არის ისეთი რთული, როგორც ჩანს. წილადი მთელ რიცხვზე რომ გაყოთ, საკმარისია მთელი რიცხვი გადააკეთოთ წილადზე, იპოვოთ წილადის საპასუხო და შედეგი გავამრავლოთ პირველ წილადზე. თუ გსურთ იცოდეთ როგორ გააკეთოთ ეს, უბრალოდ მიყევით ამ ნაბიჯებს:
ნაბიჯი
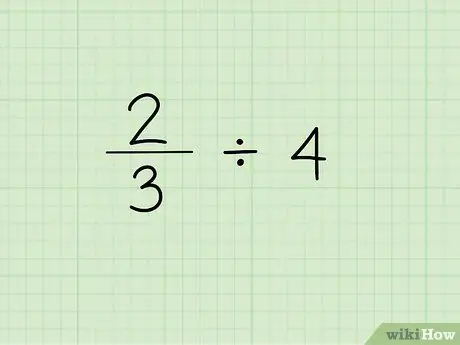
ნაბიჯი 1. ჩაწერეთ პრობლემა
წილის მთელ რიცხვზე გაყოფის პირველი ნაბიჯი არის წილადის დაწერა, რასაც მოჰყვება გაყოფის ნიშანი და მთელი რიცხვი, რომელიც საჭიროა წილადის გაყოფისათვის. ვთქვათ, ჩვენ ვმუშაობთ შემდეგ პრობლემასთან: 2/3 4.
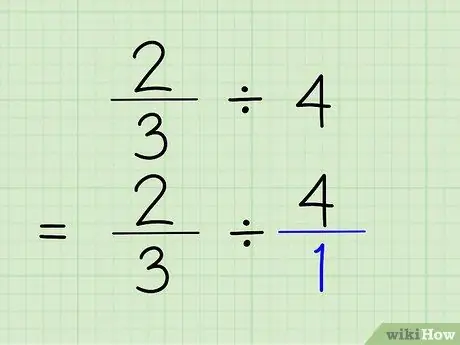
ნაბიჯი 2. გადააქციე მთელი რიცხვები წილად
მთელი რიცხვის წილად გადასაყვანად, თქვენ მხოლოდ უნდა მოათავსოთ მთელი რიცხვი ნომერზე 1. მთელი რიცხვი ხდება მრიცხველი და 1 ხდება წილადის მნიშვნელი. 4/1 თქმა ნამდვილად იგივეა, რაც 4 -ის თქმა, რადგან თქვენ მხოლოდ აჩვენებთ, რომ რიცხვი შეიცავს "1" 4 -ჯერ. პრობლემა იქნება 2/3 4/1.
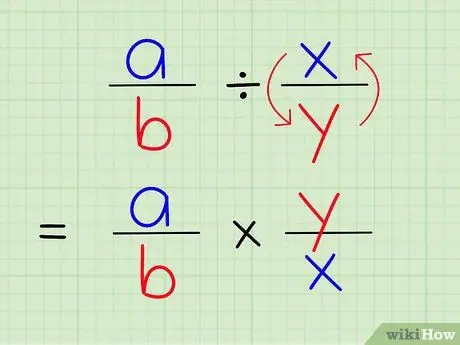
ნაბიჯი 3. წილადის გაყოფა მეორეზე იგივეა, რაც ეს წილადი გამრავლდეს სხვა წილადის საპასუხოდ
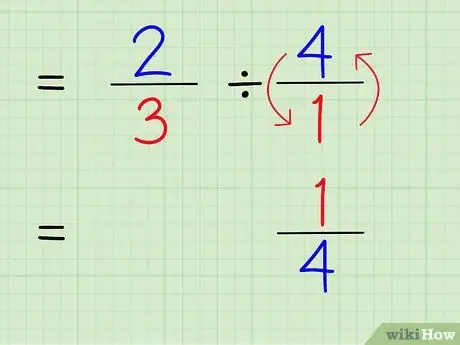
ნაბიჯი 4. ჩაწერეთ მთელი რიცხვის საპასუხო
რიცხვის ორმხრივი საპოვნელად, შეცვალეთ რიცხვის მრიცხველი და მნიშვნელი. ამიტომ, 4/1 – ის საპასუხოდ, უბრალოდ შეცვალეთ მრიცხველი და მნიშვნელი ისე, რომ რიცხვი გახდეს 1/4.
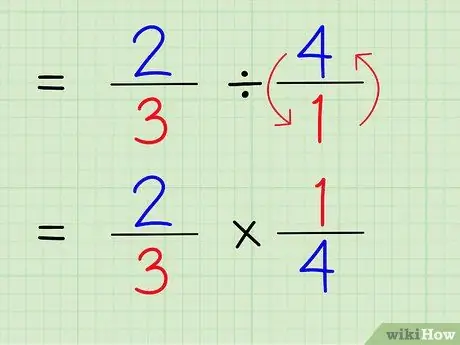
ნაბიჯი 5. შეცვალეთ გაყოფის ნიშანი გამრავლების ნიშანზე
პრობლემა იქნება 2/3 x 1/4.
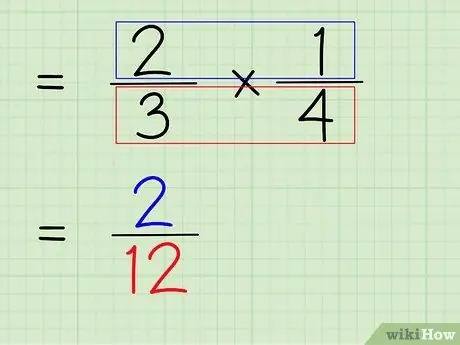
ნაბიჯი 6. გავამრავლოთ წილადის მრიცხველი და მნიშვნელი
ასე რომ, შემდეგი ნაბიჯი არის წილადის მრიცხველისა და მნიშვნელის გამრავლება, რათა მივიღოთ ახალი მრიცხველი და მნიშვნელი, როგორც საბოლოო პასუხი.
- მრიცხველების გასამრავლებლად, უბრალოდ გამრავლდით 2 x 1, რომ მიიღოთ 2.
- მნიშვნელი რომ გავამრავლოთ, უბრალოდ გავამრავლოთ 3 x 4, რომ მივიღოთ 12.
- 2/3 x 1/4 = 2/12
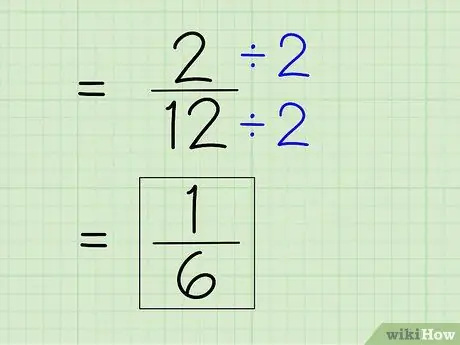
ნაბიჯი 7. გაამარტივეთ წილადი
წილადის გასამარტივებლად თქვენ უნდა იპოვოთ ყველაზე პატარა მნიშვნელი, რაც ნიშნავს რომ მრიცხველი და მნიშვნელი უნდა გაყოთ ნებისმიერ რიცხვზე, რომელიც ორივე რიცხვს ყოფს. ვინაიდან 2 არის მრიცხველი, თქვენ უნდა ნახოთ, შეუძლია თუ არა 2 სრულად გაყოს 12 - ეს შესაძლებელია, რადგან 12 არის ლუწი რიცხვი. შემდეგ გაყავით მრიცხველი და მნიშვნელი 2 -ზე, რომ მიიღოთ ახალი მრიცხველი და მნიშვნელი მარტივი პასუხის მისაღებად.
- 2 ÷ 2 = 1
- 12 ÷ 2 = 6
- წილადი 2/12 შეიძლება გამარტივდეს 1/6. ეს არის თქვენი საბოლოო პასუხი.
Რჩევები
- ეს არის მეხსიერების გასაადვილებლად, მარტივი გზა დაიმახსოვროთ, როგორ გავაკეთოთ ყველა ეს გამოთვლა. გაითვალისწინეთ ეს: "ადვილია წილადების გაყოფა, მეორე რიცხვის გადაბრუნება და გამრავლება!"
- ზემოაღნიშნული მეთოდის სხვა ვარიაციაა JGB/JBG. არ შეცვალოთ პირველი ნომერი. შეცვლა გამრავლებაზე. გადააბრუნეთ ბოლო რიცხვი. ან B ჯერ G შემდეგ
- თუ თქვენ გააუქმებთ გაანგარიშებას მის გამრავლებამდე, შეიძლება არ დაგჭირდეთ წილადის უმარტივესი ფორმის პოვნა, რადგან შედეგი უკვე არის უმარტივეს წილადის სახით, როგორც ხედავთ. ჩვენს მაგალითში, სანამ გავამრავლებთ 2/3 × 1/4, ჩვენ შეგვიძლია დავინახოთ, რომ პირველ მრიცხველს (2) და მეორე მნიშვნელს (4) აქვს ერთი და იგივე გამრავლება 2, რომელიც შეგვიძლია გავაუქმოთ სანამ გავაგრძელებთ გამოთვლას. ეს გადააქცევს პრობლემას 1/3 × 1/2, რაც იძლევა დაუყოვნებლივ 1/6 შედეგს და დაზოგავს დროს, რათა გავამარტივოთ წილადი შემდგომ ეტაპზე.
- თუ თქვენი ერთ -ერთი ფრაქცია უარყოფითია, ეს მეთოდი მაინც გამოსადეგია; დარწმუნდით, რომ თვალყურს ადევნებთ ნიშნებს ამ ნაბიჯების შესრულებისას.
