- ავტორი Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-19 22:13.
- ბოლოს შეცვლილი 2025-06-01 06:06.
მათემატიკა რთულია. ადვილია დაივიწყო თუნდაც ძირითადი ცნებები, როცა ცდილობ მრავალი განსხვავებული პრინციპის და მეთოდის გახსენებას. აქ მოცემულია წილადების გამარტივების ორი ახალი გზა.
ნაბიჯი
მეთოდი 1 4 -დან: უდიდესი საერთო ფაქტორის გამოყენება

ნაბიჯი 1. ჩამოწერეთ მრიცხველი და მნიშვნელი ფაქტორები
ფაქტორები არის რიცხვები, რომელთა გამრავლება შეგიძლიათ სხვა რიცხვის მისაღებად. მაგალითად, 3 და 4 არის 12 - ის ფაქტორი, რადგან თქვენ შეგიძლიათ გაამრავლოთ ისინი ერთად, რათა მიიღოთ 12, რიცხვის ფაქტორების ჩამოსაწერად, თქვენ უბრალოდ უნდა ჩამოწეროთ ყველა რიცხვი, რომელიც შეიძლება გამრავლდეს ამ რიცხვის მისაღებად და იყოფა. ფაქტორებით.
-
ჩაწერეთ რიცხვის ფაქტორები უმცირესიდან უმსხვილესზე, არ დაგავიწყდეთ ფაქტორის 1. ჩართვა. მაგალითად, აი როგორ წერთ წილადის მრიცხველს და მნიშვნელს 24/32:
- 24: 1, 2, 3, 4, 6, 8, 12, 24.
- 32: 1, 2, 4, 8, 16, 32.

ნაბიჯი 2. იპოვეთ მრიცხველისა და მნიშვნელის უდიდესი საერთო ფაქტორი (GCF)
GCF არის ყველაზე დიდი რიცხვი, რომელსაც შეუძლია თანაბრად გაყოს ორი ან მეტი რიცხვი. მას შემდეგ რაც ჩაწერეთ რიცხვის ყველა ფაქტორი, თქვენ მხოლოდ უნდა იპოვოთ ყველაზე დიდი რიცხვი, რომელიც ერთნაირია ფაქტორების ორივე სიაში.
-
24: 1, 2, 3, 4, 6,
ნაბიჯი 8., 12, 24.
-
32: 1, 2, 4,
ნაბიჯი 8., 16, 32.
-
GCF 24 და 32 არის 8, რადგან 8 არის ყველაზე დიდი რიცხვი, რომელსაც შეუძლია თანაბრად გაყოს 24 და 32.

ნაბიჯი 3. გაყავით მრიცხველი და წილადი GCF- ზე
ახლა, როდესაც თქვენ გაქვთ GCF, თქვენ მხოლოდ უნდა გაყოთ მრიცხველი და მნიშვნელი ამ რიცხვზე, რათა გაამარტივოთ თქვენი წილა მისი უმარტივესი ფორმით. აქ მოცემულია როგორ გავაკეთოთ ეს:
- 24/8 = 3
- 32/8 = 4
- მარტივი წილადია 3/4.

ნაბიჯი 4. შეამოწმეთ თქვენი სამუშაო
თუ გსურთ დარწმუნდეთ, რომ თქვენ სწორად გაამარტივეთ წილადი, თქვენ უბრალოდ უნდა გაამრავლოთ ახალი მრიცხველი და მნიშვნელი მათი GCF- ით, რომ მიიღოთ ორიგინალური წილადი. აქ მოცემულია როგორ გავაკეთოთ ეს:
- 3 * 8 = 24
- 4 * 8 = 32
-
თქვენ დაუბრუნდით პირვანდელ ფორმას, რომელიც არის 24/32.
თქვენ ასევე შეგიძლიათ შეამოწმოთ წილადი, რათა დარწმუნდეთ, რომ მისი შემდგომი გამარტივება შეუძლებელია. ვინაიდან 3 არის პირველადი რიცხვი, ის შეიძლება დაიყოს მხოლოდ 1 -ით და თავისთავად, ხოლო ოთხი არ იყოფა 3 -ზე, ამიტომ წილადის შემდგომი გამარტივება შეუძლებელია
მეთოდი 2 -დან 4 -დან: განაგრძეთ მცირე რიცხვებით გაყოფა

ნაბიჯი 1. აირჩიეთ მცირე რიცხვი
ამ მეთოდის გამოყენებით, თქვენ უნდა აირჩიოთ მხოლოდ მცირე რიცხვი, როგორიცაა 2, 3, 4, 5 ან 7, რომ დაიწყოთ. შეხედეთ წილადებს და დარწმუნდით, რომ თითოეული ნაწილი იყოფა თქვენს მიერ არჩეულ რიცხვზე. მაგალითად, თუ თქვენ გაქვთ წილადი 24/108, არ აირჩიოთ 5, რადგან ისინი არ იყოფა 5 -ზე. თუმცა, თუ თქვენ გაქვთ წილადი 25/60, 5 არის სწორი რიცხვი გამოსაყენებლად.
წილადისთვის 24/32, 2 კარგი რიცხვია. ვინაიდან ორივე რიცხვი ლუწი რიცხვია, ისინი იყოფა 2 -ზე

ნაბიჯი 2. წილადის მრიცხველი და მნიშვნელი გავყოთ რიცხვზე
ახალი წილადი შედგება ახალი მრიცხველისა და მნიშვნელისაგან, რომელსაც მიიღებთ წილადის ზედა და ქვედა 24/32 -ზე გაყოფის შემდეგ 2. აი, როგორ გავაკეთოთ ეს:
- 24/2 = 12
- 32/2 = 16
- თქვენი ახალი ფრაქცია არის 12/16.
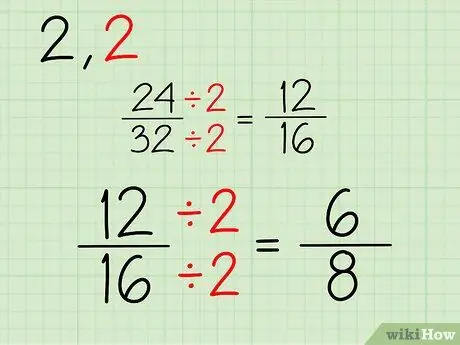
ნაბიჯი 3. გაიმეორეთ
გააგრძელე ეს პროცესი. ვინაიდან ორივე რიცხვი ლუწი რიცხვია, შეგიძლიათ განაგრძოთ გაყოფა 2 - ზე. თუ ერთი ან ორივე მრიცხველი და მნიშვნელი კენტი რიცხვებია, მაშინ შეგიძლიათ სცადოთ სხვა რიცხვზე გაყოფა. აქ მოცემულია პროცესი 12/16 წილის გამარტივების მიზნით:
- 12/2 = 6
- 16/2 = 8
- თქვენი ახალი ფრაქცია არის 6/8.

ნაბიჯი 4. განაგრძეთ რიცხვის გაყოფა მანამ, სანამ ის აღარ იყოფა
ახალი მრიცხველი და მნიშვნელი ასევე არის რიცხვები, ასე რომ თქვენ შეგიძლიათ განაგრძოთ გაყოფა 2 -ზე. აი როგორ უნდა გავაკეთოთ ეს:
- 6/2 = 3
- 8/2 = 4
- თქვენი ახალი ფრაქცია არის 3/4.

ნაბიჯი 5. დარწმუნდით, რომ წილის შემდგომი გამარტივება შეუძლებელია
წილადში 3/4, 3 არის პირველადი რიცხვი, ამიტომ ფაქტორები მხოლოდ 1 და თავად არის, ხოლო 4 არ იყოფა 3 -ზე, ამიტომ წილადის შემდგომი გამარტივება შეუძლებელია. თუ წილადის მრიცხველი ან მნიშვნელი ვეღარ იყოფა თქვენს მიერ არჩეულ რიცხვზე, თქვენ მაინც შეძლებთ მის გაყოფას სხვა რიცხვზე.
მაგალითად, თუ თქვენ გაქვთ წილადი 10/40 და გაყოფთ მრიცხველსა და მნიშვნელს 5 -ზე, შედეგი არის 2/8. თქვენ არ შეგიძლიათ გაყოთ მრიცხველი და წილადი 5 -ზე, მაგრამ შეგიძლიათ გაყოთ ორივე 2 -ზე, ასე რომ საბოლოო შედეგი არის 1/4

ნაბიჯი 6. შეამოწმეთ თქვენი სამუშაო
გაამრავლეთ 3/4 2/2 სამჯერ კიდევ ერთხელ, რათა დარწმუნდეთ რომ მიიღებთ საწყის წილადს, რომელიც არის 24/32. აქ მოცემულია როგორ გავაკეთოთ ეს:
- 3/4 * 2/2 = 6/8
- 6/8 * 2/2 = 12/16
- 12/16 * 2/2 = 24/32.
- გაითვალისწინეთ, რომ თქვენ 24/32 გაყოფთ 2 * 2 * 2 -ზე, რაც იგივეა, რაც 8 -ზე, 24 და 32 -ის უდიდესი GCF.
მეთოდი 3 დან 4: ფაქტორების წერა

ნაბიჯი 1. ჩაწერეთ თქვენი წილადი
დატოვეთ დიდი ადგილი თქვენი ქაღალდის მარჯვენა მხარეს - ეს დაგჭირდებათ ფაქტორების ჩამოსაწერად.

ნაბიჯი 2. ჩამოწერეთ მრიცხველისა და მნიშვნელის ფაქტორები
მარტო ორივეს ფაქტორი. უმარტივესი გზაა ის ფაქტორები, რომლებიც ერთმანეთზეა დაწერილი. დაიწყეთ ნომრით 1 და ჩამოწერეთ ფაქტორები.
-
მაგალითად, თუ თქვენი ფრაქცია არის 24/60, დაიწყეთ 24 -ით.
ჩამოწერეთ: 24 - 1, 2, 3, 4, 6, 8, 12, 24
-
შემდეგ რიცხვი 60.
ჩამოწერეთ: 60 - 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60

ნაბიჯი 3. იპოვეთ და გაყავით უდიდესი საერთო ფაქტორით
ეს ტერმინი შეიძლება ჩაწერილი იყოს როგორც GCF თქვენს დაბეჭდილ წიგნში. რა არის ყველაზე დიდი რიცხვი, რომელსაც შეუძლია გაანგარიშოს მრიცხველი და მნიშვნელი? როგორი რიცხვიც არ უნდა იყოს, ორივე რიცხვი გაყავით ამ რიცხვზე.
ჩვენი მაგალითისთვის, ყველაზე დიდი რიცხვი, რომელიც არის ორივე რიცხვის ფაქტორი, არის 12. ასე რომ, ჩვენ 24 -ს ვყოფთ 12 -ზე და 60 -ს 12 -ზე, რაც გვაძლევს 2/5 - ჩვენი მარტივი წილადი
მეთოდი 4 -დან 4: ძირითადი ფაქტორული ხის გამოყენება

ნაბიჯი 1. იპოვეთ მრიცხველისა და მნიშვნელის ძირითადი ფაქტორები
მარტივი რიცხვი არის რიცხვი, რომელიც არ შეიძლება გაიყოს სხვა რიცხვზე (რა თქმა უნდა, თავის და 1 -ის გარდა). 2, 3, 5, 7 და 11 არის მარტივი რიცხვების მაგალითები.
- დაიწყეთ მრიცხველით. 24 -დან, გაყავით 2 -სა და 12. -ზე, ვინაიდან 2 უკვე პირველი რიცხვია, თქვენ აღარ გჭირდებათ მისი გაყოფა! შემდეგ გაყავით 12 ორ რიცხვში: 2 და 6. 2 არის მარტივი რიცხვები - შესანიშნავია! ახლა გაყავით 6 ორ რიცხვში: 2 და 3. ახლა თქვენ გაქვთ 2, 2, 2 და 3 თქვენი ძირითადი რიცხვები.
- ახლა იმუშავეთ მნიშვნელზე. 60 -დან, გაყავით თქვენი ხე 2 და 30. 30 შემდეგ გაყავით 2 და 15. შემდეგ გაყავით 15 3 და 5, ორივე მათგანი მარტივი რიცხვებია. ახლა თქვენ გაქვთ 2, 2, 3 და 5, როგორც თქვენი ძირითადი რიცხვები.
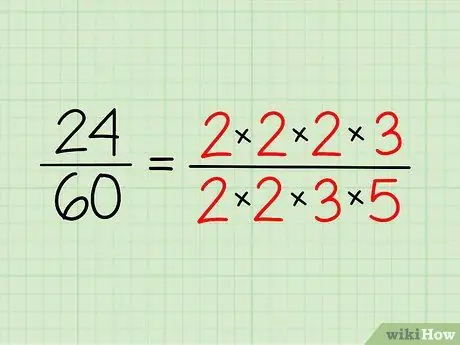
ნაბიჯი 2. ჩაწერეთ თითოეული რიცხვის ძირითადი ფაქტორიზაცია
ჩამოწერეთ თითოეული რიცხვისთვის განკუთვნილი მარტივი რიცხვები და ჩაწერეთ გამრავლების სახით. თქვენ არ გჭირდებათ მისი გამრავლება - ეს მხოლოდ გზაა, რომ გაადვილოთ დანახვა.
- ასე რომ, 24 -ისთვის თქვენ გაქვთ 2 x 2 x 2 x 3 = 24.
- 60 -ისთვის თქვენ გაქვთ 2 x 2 x 3 x 5 = 60

ნაბიჯი 3. აღმოფხვრა იგივე ფაქტორები
ნებისმიერი რიცხვი, რომელიც ორივე რიცხვის ნაწილია, შეიძლება გაუქმდეს. ამ მაგალითში თანაბარი ფაქტორებია წყვილი 2 და ერთი 3. ნახვამდის!
- დანარჩენი არის 2 და 5 - ან 2/5! იგივე პასუხი მივიღეთ ზემოთ.
- თუ წილადის მრიცხველი და მნიშვნელი არის რიცხვები, ნუ გაყოფთ მხოლოდ ორზე. განაგრძეთ გაყოფის გაკეთება, სანამ მიღებული რიცხვი კვლავ არ გაიყოფა.






