სპირმანის რანგის კორელაციის კოეფიციენტის გამოთვლის 3 გზა

2024 ავტორი: Jason Gerald | [email protected]. ბოლოს შეცვლილი: 2023-12-16 11:21

სპირმანის რანგის კორელაციის კოეფიციენტით შეგვიძლია დავადგინოთ აქვს თუ არა ორ ცვლადს ერთფეროვანი ფუნქციური კავშირი (ანუ როდესაც ერთი რიცხვი იზრდება, მეორე რიცხვიც გაიზრდება, ან პირიქით). სპირმანის რანგის კორელაციის კოეფიციენტის გამოსათვლელად, თქვენ უნდა დაალაგოთ და შეადაროთ მონაცემთა ნაკრები დ²და შემდეგ შეიყვანეთ მონაცემები სტანდარტული ან გამარტივებული სპირმანის რანგის კორელაციის კოეფიციენტის ფორმულაში. თქვენ ასევე შეგიძლიათ გამოთვალოთ ეს კოეფიციენტები Excel ფორმულების ან R ბრძანების გამოყენებით.

ნაბიჯი

მეთოდი 1 -დან 3 -დან: ხელით

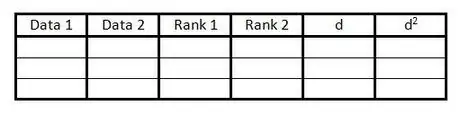
ნაბიჯი 1. შექმენით ცხრილი

ცხრილი გამოიყენება ყველა ინფორმაციის შესაქმნელად, რაც საჭიროა სპირმენის რანგის კორელაციის კოეფიციენტის გამოსათვლელად. თქვენ გჭირდებათ ასეთი მაგიდა:

• შექმენით 6 სვეტი სათაურებით, როგორც მაგალითში.
• მოამზადეთ იმდენი ცარიელი სტრიქონი, რამდენიც მონაცემთა წყვილების რაოდენობა.

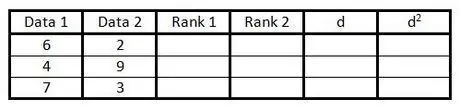
ნაბიჯი 2. შეავსეთ პირველი ორი სვეტი მონაცემთა წყვილით

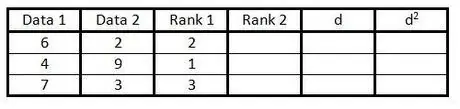
ნაბიჯი 3. შეიყვანეთ მონაცემთა ჯგუფის პირველი სვეტის რეიტინგი მესამე სვეტში 1 -დან n- მდე (მონაცემების რაოდენობა)

მიეცით ნიშანი 1 ყველაზე დაბალი მნიშვნელობისათვის, ნიშანი 2 შემდეგი ყველაზე დაბალი მნიშვნელობისთვის და ასე შემდეგ.

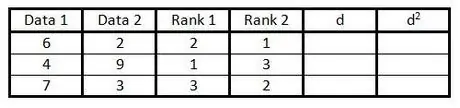
ნაბიჯი 4. მეოთხე სვეტში გააკეთეთ იგივე, რაც მე –3 საფეხურზე, მაგრამ მონაცემები მეორე სვეტში განათავსეთ

• 

  თუ არსებობს ორი (ან მეტი) მონაცემი, რომელსაც აქვს იგივე მნიშვნელობა, გამოთვალეთ მონაცემების საშუალო რეიტინგი და შემდეგ ჩაწერეთ იგი ცხრილში ამ საშუალო მნიშვნელობის საფუძველზე.

  მაგალითში მარჯვნივ, არის ორი მნიშვნელობა 5 რეიტინგებზე 2 და 3. ვინაიდან არსებობს ორი 5, იპოვეთ რეიტინგების საშუალო. საშუალო 2 და 3 არის 2.5, ასე რომ შეიყვანეთ შეფასების მნიშვნელობა 2.5 ორივე მნიშვნელობისთვის 5.

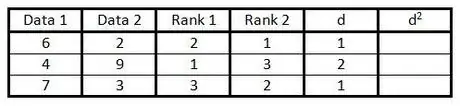
ნაბიჯი 5. სვეტში "დ" გამოთვალეთ სხვაობა რანგის სვეტის ორ რიცხვს შორის

ანუ, თუ ერთი სვეტი არის 1 ადგილზე და მეორე სვეტი არის 3 ადგილზე, სხვაობა არის 2. (ნიშანს არ აქვს მნიშვნელობა, რადგან შემდეგი ნაბიჯი არის მნიშვნელობის კვადრატი.)

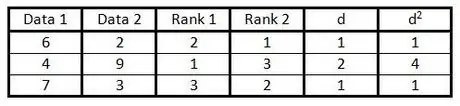
ნაბიჯი 6. მოათავსეთ თითოეული რიცხვი სვეტში "დ" და ჩაწერეთ შედეგი სვეტში "დ"²".

ნაბიჯი 7. დაამატეთ ყველა მონაცემი სვეტში დ²".

შედეგი არის დ².

ნაბიჯი 8. აირჩიეთ ერთი შემდეგი ფორმულადან:

• თუ არცერთი რეიტინგი არ არის იგივე რაც წინა საფეხურზე, შეიყვანეთ ეს მნიშვნელობა გამარტივებული Spearman რანგის კორელაციის კოეფიციენტის ფორმულაში

  

  და შედეგის მისაღებად შეცვალეთ "n" მონაცემთა წყვილების რაოდენობით.

  

• თუ წინა საფეხურზე არის მსგავსი წოდება, გამოიყენეთ სტანდარტული Spearman რანგის კორელაციის კოეფიციენტის ფორმულა:

  

ნაბიჯი 9. შედეგების ინტერპრეტაცია

მნიშვნელობა შეიძლება განსხვავდებოდეს -1 -დან 1 -მდე.

• თუ მნიშვნელობა ახლოს არის -1, კორელაცია უარყოფითია.
• თუ მნიშვნელობა არის 0 -თან ახლოს, არ არსებობს წრფივი კორელაცია.
• თუ მნიშვნელობა 1 -თან ახლოს არის, კორელაცია დადებითია.

3 მეთოდი 2: Excel– ის გამოყენება

ნაბიჯი 1. შექმენით მონაცემების ახალი სვეტი მის რეიტინგთან ერთად

მაგალითად, თუ თქვენი მონაცემები არის სვეტში A2: A11, გამოიყენეთ ფორმულა "= RANK (A2, A $ 2: A $ 11)" და დააკოპირეთ სანამ არ მოიცავს ყველა სვეტს და რიგებს.

ნაბიჯი 2. შეცვალეთ იგივე ნიშანი, როგორც აღწერილია 1 მეთოდის მე –3 და მე –4 ნაბიჯებში

ნაბიჯი 3. ახალ უჯრედში გამოთვალეთ კორელაცია ორ წოდებულ სვეტს შორის ფორმულთან "= CORREL (C2: C11, D2: D11)"

ამ მაგალითში C და D ეხება სვეტს, სადაც რეიტინგი მდებარეობს. ახალი უჯრედი შეივსება სპირმენის რანგის კორელაციით.

მეთოდი 3 3 -დან: რ

ნაბიჯი 1. დააინსტალირეთ R პროგრამა ჯერ თუ უკვე არ გაქვთ

(იხილეთ

ნაბიჯი 2. შეინახეთ თქვენი მონაცემები CSV ფორმაში, განათავსეთ მონაცემები, რომელთაც გსურთ იპოვოთ კორელაცია პირველ ორ სვეტში

ჩვენ შეგვიძლია ამის გაკეთება "შენახვა როგორც" მენიუს გამოყენებით.

ნაბიჯი 3. გახსენით R Editor

თუ თქვენ მუშაობთ ტერმინალიდან, უბრალოდ გაუშვით R. თუ დესკტოპიდან მუშაობთ, დააწკაპუნეთ R ხატულაზე.

ნაბიჯი 4. ჩაწერეთ შემდეგი ბრძანება:

• d <- წაიკითხე. csv ("NAME_OF_YOUR_CSV.csv") და დააჭირეთ Enter.
• მსახიობი (წოდება (დ [, 1]), წოდება (დ [, 2]))

Რჩევები

მონაცემები უნდა შედგებოდეს არანაკლებ 5 წყვილისაგან ისე, რომ ტენდენცია იყოს ხილული (მონაცემების რაოდენობა 3 წყვილია მაგალითში მხოლოდ გათვლების გასამარტივებლად.)

გაფრთხილება

• სპირმანის რანგის კორელაციის კოეფიციენტი მხოლოდ განსაზღვრავს კორელაციის სიძლიერეს, სადაც მონაცემები თანმიმდევრულად იზრდება ან მცირდება. თუ არსებობს სხვა ტენდენცია მონაცემებში, სპირმანის რანგის კორელაცია არა უზრუნველყოფს ზუსტ წარმოდგენას.
• ეს ფორმულა ემყარება იმ ვარაუდს, რომ არ არსებობს თანაბარი რეიტინგები. როდესაც არის იგივე რანგი, როგორც მაგალითში, ჩვენ უნდა გამოვიყენოთ ეს განმარტება: გამრავლების მომენტის კორელაციის კოეფიციენტი რანგის მიხედვით.