IQR არის მონაცემთა კრებულის კვარტალთა დიაპაზონი ან კვარტილური ფესვის დიაპაზონი. IQR გამოიყენება სტატისტიკურ ანალიზში მონაცემთა ნაკრების შესახებ დასკვნების დასახმარებლად. IQR უფრო ხშირად გამოიყენება ვიდრე დიაპაზონი, რადგან IQR არ შეიცავს გარე მონაცემებს. განაგრძეთ კითხვა, რომ გაიგოთ როგორ იპოვოთ IQR!
ნაბიჯი
3 მეთოდი 1: IQR– ის გაგება
ნაბიჯი 1. გაიგეთ როგორ გამოიყენოთ IQR
ძირითადად, IQR არის რიცხვების ერთობლიობის გავრცელების გაგების გზა. ძირეული კვარტილის დიაპაზონი განისაზღვრება, როგორც სხვაობა მონაცემთა ნაკრების ზედა კვარტილს (25% ზედა) და ქვედა კვარტილს შორის (25% ყველაზე დაბალი).
რჩევა:
ქვედა კვარტილი ჩვეულებრივ იწერება როგორც Q1, ხოლო ზედა კვარტილი იწერება როგორც Q3 - რაც ტექნიკურად ხდის მონაცემების შუა წერტილს Q2 და ყველაზე მაღალ წერტილს Q4.
ნაბიჯი 2. გაიაზრეთ კვარტილები
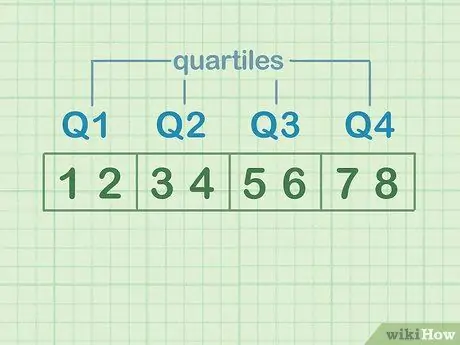
კვარტლების საილუსტრაციოდ, რიცხვების ნაკრები ოთხ თანაბარ ნაწილად გაყავით. თითოეული ეს ნაწილი არის "კვარტილი". დავუშვათ, მონაცემთა ნაკრებია: 1, 2, 3, 4, 5, 6, 7, 8.
- 1 და 2 არის პირველი კვარტილი ან Q1
- 3 და 4 არის მეორე კვარტილი ან Q2
- 5 და 6 არის მესამე კვარტილი ან Q3
- 7 და 8 არის მეოთხე კვარტილი ან Q4
ნაბიჯი 3. ისწავლეთ ფორმულა
ზედა და ქვედა კვარტილებს შორის განსხვავების საპოვნელად, თქვენ უნდა გამოაკლოთ 75 -ე პერცენტილი 25 -ე პერცენტილისგან.
ფორმულა წერია: Q3 - Q1 = IQR
მეთოდი 2 დან 3: მონაცემთა ნაკრების შედგენა
ნაბიჯი 1. შეაგროვეთ თქვენი მონაცემები
თუ თქვენ სწავლობთ IQR კლასს და ტესტებს, შეიძლება მოგეცით უკვე მომზადებული მონაცემების ნაკრები, მაგალითად 1, 4, 5, 7, 10. ეს არის თქვენი მონაცემთა ნაკრები - რიცხვები, რომლებთანაც იმუშავებთ. თუმცა, თქვენ შეგიძლიათ ააწყოთ თქვენი საკუთარი რიცხვები ცხრილის კითხვებიდან ან სიუჟეტის პრობლემებიდან.
დარწმუნდით, რომ თითოეული რიცხვი ერთსა და იმავეს ნიშნავს:
მაგალითად, კვერცხების რაოდენობა განსაზღვრულ ფრინველთა პოპულაციის თითოეულ ბუდეში, ან თითოეულ სახლში განთავსებული პარკინგის ადგილები განსაზღვრულ ბლოკში.
ნაბიჯი 2. დაალაგეთ თქვენი მონაცემები ზრდადი თანმიმდევრობით
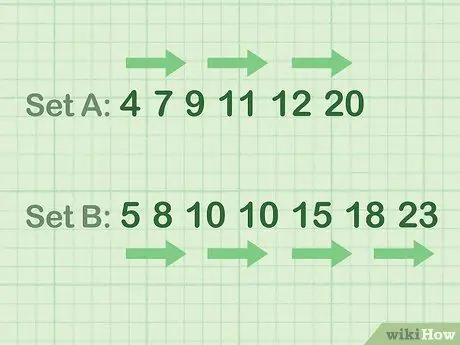
სხვა სიტყვებით რომ ვთქვათ: მოაწყეთ რიცხვები უმცირესიდან უფრო დიდამდე. გამოიყენეთ მინიშნებები შემდეგი მაგალითებიდან.
- ლუწ რიცხვთა მონაცემების მაგალითი (კომპლექტი A): 4 7 9 11 12 20
- კენტი რიცხვების მონაცემების მაგალითი (კომპლექტი B): 5 8 10 10 15 18 23 23
ნაბიჯი 3. გაყავით მონაცემები ორად
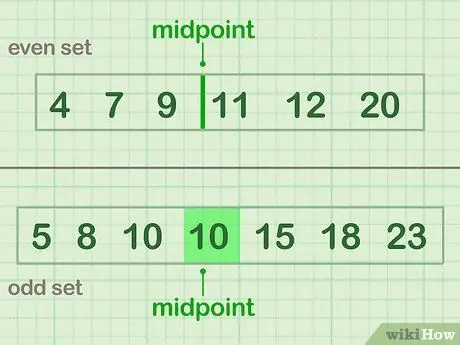
შუაზე გაყოფისთვის, იპოვეთ თქვენი მონაცემების შუა წერტილი: რიცხვი ან რიცხვები, რომლებიც მონაცემთა ნაკრების ცენტრშია. თუ თქვენ გაქვთ მონაცემების კენტი რაოდენობა, აირჩიეთ რიცხვი, რომელიც შუაშია. თუ თქვენ გაქვთ მონაცემების ლუწი რაოდენობა, შუა წერტილი არის ორ ყველაზე საშუალო რიცხვს შორის.
- თანაბარი მაგალითი (კომპლექტი A), რომელსაც აქვს შუალედი 9 -დან 11 -მდე: 4 7 9 | 11 12 20
- უცნაური მაგალითი (კომპლექტი B) რომელსაც აქვს მნიშვნელობის საშუალო წერტილი (10): 5 8 10 (10) 15 18 23
მეთოდი 3 3: IQR გამოთვლა
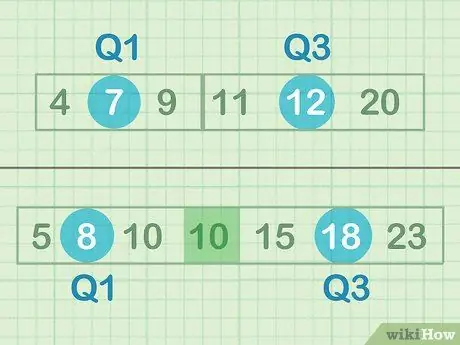
ნაბიჯი 1. იპოვეთ მონაცემთა ქვედა და ზედა ნახევრის მედიანა
მედიანა არის "შუა წერტილი" ან რიცხვი, რომელიც რიცხვების ნაკრების შუაშია. ამ შემთხვევაში, თქვენ არ ეძებთ ყველა რიცხვის შუალედს, არამედ ეძებთ ზედა და ქვედა მონაცემთა ქვეჯგუფების ფარდობით შუალედს. თუ თქვენ გაქვთ მონაცემების კენტი რაოდენობა, არ შეიტანოთ შუა რიცხვი - მაგალითად, კომპლექტში B, თქვენ არ გჭირდებათ ერთ 10 – ის ჩართვა.
-
თუნდაც მაგალითი (კომპლექტი A):
- მონაცემთა ქვედა ნახევრის საშუალო = 7 (Q1)
- მონაცემთა ზედა ნახევრის საშუალო = 12 (Q3)
-
უცნაური მაგალითი (კომპლექტი B):
- მონაცემთა ქვედა ნახევრის საშუალო = 8 (Q1)
- მონაცემთა ზედა ნახევრის საშუალო = 18 (Q3)
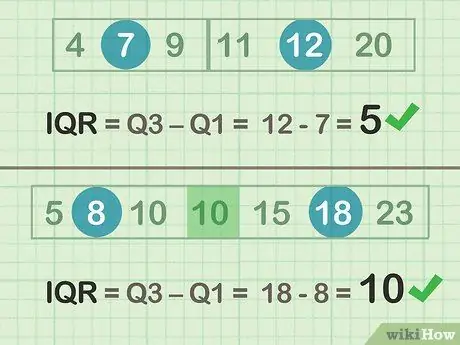
ნაბიჯი 2. გამოაკლეთ Q3-Q1 IQR- ის დასადგენად
ახლა თქვენ იცით რამდენი რიცხვი მოდის 25 -დან 75 -ე პროცენტულებს შორის. თქვენ შეგიძლიათ გამოიყენოთ ეს რიცხვი მონაცემების გავრცელების გასაგებად. მაგალითად, თუ ტესტს აქვს მაქსიმალური ქულა 100, ხოლო ქულის IQR არის 5, შეგიძლიათ ვივარაუდოთ, რომ გამოცდაზე გასული ადამიანების უმეტესობას აქვს თითქმის იგივე გაგება, რადგან მაღალი და დაბალი დონის დიაპაზონი არ არის ძალიან დიდი. თუმცა, თუ ტესტის ქულის IQR არის 30, შეიძლება გაგიკვირდეთ, რატომ იტანს ზოგი ადამიანი ასე მაღალს, ზოგი კი ასე დაბალს.
- თუნდაც მაგალითი (კომპლექტი A): 12 -7 = 5
- უცნაური მაგალითი (კომპლექტი B): 18 - 8 = 10
Რჩევები
მნიშვნელოვანია ვისწავლოთ ამის გაკეთება საკუთარ თავზე. ამასთან, არსებობს რამოდენიმე ონლაინ IQR გამომთვლელი, რომლითაც შეგიძლიათ შეამოწმოთ თქვენი სამუშაო. ძალიან ნუ დაეყრდნობით კალკულატორის პროგრამებს, თუ ამას კლასში ისწავლით! თუ თქვენ მოგეთხოვებათ IQR– ის გამოცდა, თქვენ უნდა იცოდეთ როგორ იპოვოთ იგი ხელით
დაკავშირებული WikiHow
- როგორ გამოვავლინოთ უკიდურესობა
- როგორ გამოვთვალოთ მონაცემთა ნაკრების დიაპაზონი
- როგორ გააკეთოთ ყუთი და კარვის დიაგრამა
