- ავტორი Jason Gerald gerald@how-what-advice.com.
- Public 2024-01-15 08:18.
- ბოლოს შეცვლილი 2025-06-01 06:06.
ათობითი რიცხვების გაყოფა თავიდან რთულად გამოიყურება, რადგან არავინ გასწავლათ "0, 7 -ჯერ ცხრილი". ამის საიდუმლო არის გაყოფის პრობლემის გადაყვანა ფორმატში, რომელიც იყენებს მხოლოდ მთელ რიცხვებს. მას შემდეგ რაც გადაწერთ პრობლემას ამ გზით, ის გახდება რეგულარული გრძელი გაყოფის პრობლემა.
ნაბიჯი
ნაწილი 1 2 -დან: წერის პრობლემები, როგორც ჩვეულებრივი განყოფილების პრობლემები
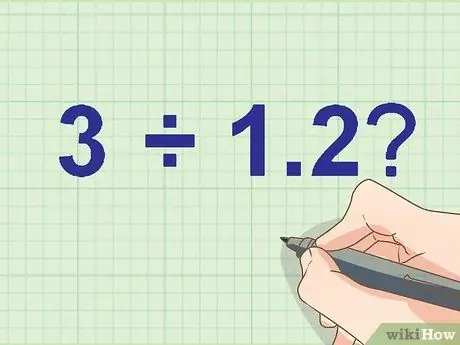
ნაბიჯი 1. ჩამოწერეთ თქვენი გაყოფის პრობლემა
გამოიყენეთ ფანქარი, თუ გსურთ გააუმჯობესოთ თქვენი სამუშაო.
-
მაგალითი:
Რამდენი 3 ÷ 1, 2?

ნაბიჯი 2. ჩაწერეთ მთელი რიცხვი ათწილადის სახით
ჩაწერეთ ათობითი წერტილი მთელი რიცხვის შემდეგ, შემდეგ ჩაწერეთ ნული ათწილადის შემდეგ. გააკეთეთ ეს მანამ, სანამ ორივე რიცხვს არ ექნება ერთი და იგივე ადგილის მნიშვნელობა ათწილადიდან მარჯვნივ. ეს არ ცვლის მთელი მნიშვნელობას.
-
მაგალითი:
ამოცანაში 3 1, 2, ჩვენი მთელი რიცხვი არის 3. ვინაიდან 1, 2 - ს აქვს ადგილის მნიშვნელობა ათწილადის მარჯვნივ, ჩაწერეთ 3 როგორც 3, 0 ისე, რომ ამ რიცხვს ასევე ჰქონდეს ერთი ადგილის მნიშვნელობა ათწილადის შემდეგ. ახლა ჩვენი საქმე ხდება 3, 0 ÷ 1, 2.
- გაფრთხილება: ნუ დაამატებთ ნულებს ათწილადის მარცხნივ! ნომერი 3 უდრის 3, 0 ან 3, 00, მაგრამ არა უდრის 30 ან 300.

ნაბიჯი 3. გადაიყვანეთ ათობითი წერტილი მარჯვნივ, სანამ არ მიიღებთ მთელ რიცხვს
გაყოფის პრობლემებში შეგიძლიათ ათწილადების გადატანა, მაგრამ მხოლოდ იმ შემთხვევაში, თუ ათვლის წერტილებს გადაინაცვლებთ ყველა რიცხვზე ერთი და იმავე რაოდენობის ნაბიჯებით. ეს საშუალებას გაძლევთ გადააკეთოთ პრობლემა მთელ რიცხვზე.
-
მაგალითი:
3, 0 1, 2 მთელ რიცხვზე გადასაყვანად, ათწილადის წერტილი გადადგით ერთი ნაბიჯი მარჯვნივ. ამრიგად, 3, 0 ხდება 30 და 1, 2 ხდება 12. ახლა, ჩვენი პრობლემა ხდება 30 ÷ 12.

ნაბიჯი 4. ჩაწერეთ პრობლემა გრძელი გაყოფის გამოყენებით
განათავსეთ გამყოფი რიცხვი (ჩვეულებრივ უფრო დიდი რიცხვი) გრძელი გაყოფის სიმბოლოს ქვეშ. ჩაწერეთ გამყოფი რიცხვი ამ სიმბოლოს მიღმა. ახლა თქვენ გაქვთ რეგულარული გრძელი გაყოფის პრობლემა, რომელიც იყენებს მთელ რიცხვებს. თუ გსურთ შეხსენება, თუ როგორ უნდა გააკეთოთ გრძელი გაყოფა, წაიკითხეთ შემდეგი ნაწილი.
მე -2 ნაწილი 2: გრძელი დაყოფის პრობლემების გადაჭრა

ნაბიჯი 1. იპოვეთ პასუხის პირველი ციფრი
დაიწყეთ ამ პრობლემის მოგვარება ისევე, როგორც ამას ჩვეულებრივ გააკეთებდით, გამყოფი და გაყოფილი რიცხვის პირველი ციფრი შეადარეთ. გამოთვალეთ პირველი ციფრის გამყოფი რიცხვის გამყოფი რიცხვის მიხედვით, შემდეგ ჩაწერეთ შედეგი ამ ციფრის ზემოთ.
მაგალითი: ჩვენ ვცდილობთ გავყოთ 30 -ზე 12. შეადარეთ 12 რიცხვის გაყოფილი რიცხვის პირველ ციფრს, რომელიც არის 3. რადგან 12 არის 3 -ზე მეტი, 3 გაყოფილი 12 -ზე უდრის 0. ჩამოწერეთ 0 3 ზე ზემოთ პასუხის ხაზში.
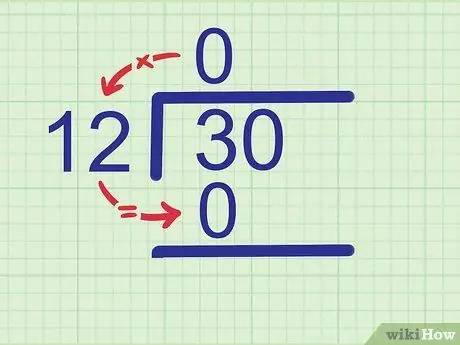
ნაბიჯი 2. გავამრავლოთ კოეფიციენტი გამყოფით
ჩაწერეთ პროდუქტის პროდუქტი გაყოფილი რიცხვის ქვეშ. ჩაწერეთ შედეგი თქვენს მიერ გაყოფილი რიცხვის პირველი ციფრის ქვემოთ, რადგან ეს არის ციფრი, რომელიც თქვენ ახლახან ნახეთ.
-
მაგალითი:
ვინაიდან 0 x 12 = 0, დაწერე 0 3 წლამდე
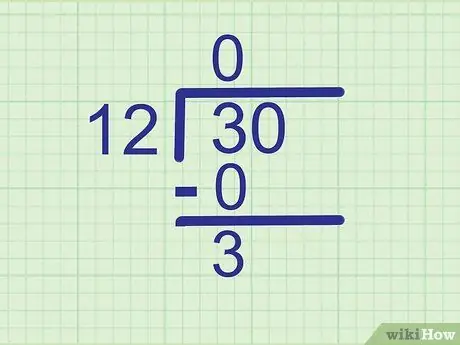
ნაბიჯი 3. გამოაკელი ნაშთის საპოვნელად
გამოაკლეთ თქვენ მიერ გამოთვლილი პროდუქტი უშუალოდ მის ზემოთ მოცემულ ციფრს. ჩაწერეთ პასუხი ახალ სტრიქონზე, მის ქვემოთ.
-
მაგალითი:
3 - 0 = 3, ასე რომ დაწერე
ნაბიჯი 3. 0 -ზე ქვემოთ
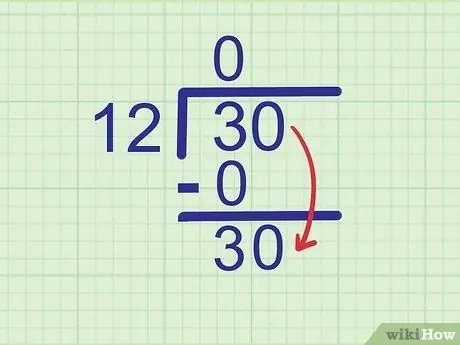
ნაბიჯი 4. შეამცირეთ შემდეგი ციფრი
ჩამოწერეთ გაყოფილი რიცხვის შემდეგი ციფრი იმ რიცხვის გვერდით, რომელიც ახლახან ჩაწერეთ.
-
მაგალითი:
რიცხვი, რომელიც იყოფა არის 30. ჩვენ ვნახეთ რიცხვი 3, ასე რომ შემდეგი ციფრი, რომელიც უნდა შემცირდეს არის 0. შეამცირეთ რიცხვი 0 3 - ის მხარეს ისე, რომ ის გახდეს
ნაბიჯი 30..
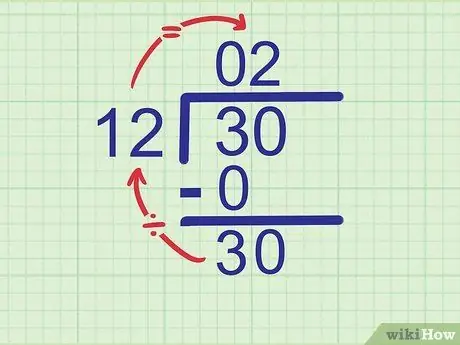
ნაბიჯი 5. სცადეთ ახალი რიცხვის გაყოფა გამყოფზე
ახლა გაიმეორეთ პირველი ნაბიჯი ამ განყოფილებაში, რომ იპოვოთ თქვენი პასუხის მეორე ციფრი. ამჯერად, შეადარეთ გამყოფი იმ რიცხვს, რომელიც ახლახან ჩაწერეთ ქვედა რიგში.
-
მაგალითი:
რა არის 30 -ის კოეფიციენტი 12 -ზე? უახლოესი პასუხი, რომელიც შეგვიძლია მივიღოთ არის 2, რადგან 12 x 2 = 24. დაწერეთ
ნაბიჯი 2. მეორე ადგილზეა პასუხის ხაზში.
- თუ არ ხართ დარწმუნებული პასუხში, სცადეთ რამდენიმე გამრავლება სანამ არ იპოვით ყველაზე დიდ პასუხს, რომელიც ჯდება. მაგალითად, თუ თქვენი შეფასება არის 3, გამოთვალეთ 12 x 3 და მიიღებთ 36. ეს რიცხვი ძალიან დიდია, რადგან ჩვენ ვცდილობთ გამოვთვალოთ 30. სცადეთ ერთი რიცხვის შემცირება, 12 x 2 = 24. ეს რიცხვი შეესაბამება. ასე რომ, 2 არის სწორი პასუხი.

ნაბიჯი 6. გაიმეორეთ ზემოაღნიშნული ნაბიჯები შემდეგი ნომრის მოსაძებნად
ეს არის იგივე გრძელი გაყოფის პროცესი, როგორც ზემოთ იყო გამოყენებული და ნებისმიერი გრძელი გაყოფის პრობლემა:
- გაამრავლეთ თქვენი პასუხის ახალი ციფრი გამყოფზე: 2 x 12 = 24.
- ჩაწერეთ პროდუქტი ახალ სტრიქონზე, იმ რიცხვის ქვემოთ, რომელიც იყოფა: ჩაწერეთ 24 მხოლოდ 30 - ზე ქვემოთ.
- ქვედა სტრიქონი გამოაკელით ზემოდან ზემოდან: 30 - 24 = 6. ასე რომ, ჩაწერეთ 6 ახალ რიგში ქვემოთ.

ნაბიჯი 7. გააგრძელეთ ეს პროცესი სანამ არ დაასრულებთ პასუხების ბოლო სტრიქონს
თუ გაყოფილ რიცხვში ჯერ კიდევ დარჩა ციფრები, შეამცირეთ ციფრები ქვემოთ და განაგრძეთ პრობლემის მოგვარება ანალოგიურად. თუ თქვენ დაასრულეთ პასუხების ბოლო ხაზი, გააგრძელეთ შემდეგი ნაბიჯი.
-
მაგალითი:
ჩვენ უბრალოდ დავწერეთ
ნაბიჯი 2. ბოლო პასუხის ხაზში. გააგრძელე შემდეგი ნაბიჯი.

ნაბიჯი 8. დაამატეთ ათწილადები, რომ საჭიროების შემთხვევაში გაზარდოთ რიცხვი
თუ რიცხვი თანაბრად იყოფა, თქვენი გამოკლების საბოლოო შედეგია „0“. ეს ნიშნავს, რომ თქვენ დაასრულეთ გაყოფა და მიიღებთ პასუხს მთელი რიცხვის სახით. თუმცა, თუ თქვენ დაასრულეთ პასუხების ბოლო სტრიქონი და ჯერ კიდევ არის ციფრები, რომლებიც შეიძლება დაიყოს, თქვენ უნდა გაზარდოთ გამყოფი რიცხვი ათწილადის დამატებით, რასაც მოჰყვება რიცხვი 0. გაითვალისწინეთ, რომ ეს არ არის არ შეცვალოთ რიცხვის მნიშვნელობა.
-
მაგალითი:
ჩვენ მივედით პასუხების ბოლო ხაზზე, მაგრამ პასუხი ჩვენს ბოლო გამოკლებაზე არის "6". ჩაწერეთ „6, 0“გრძელი გაყოფის სიმბოლოს ბოლო ციფრზე „, 0“დამატებით. ასევე ჩაწერეთ ათწილადის წერტილი იმავე ადგილას პასუხის ხაზზე, მაგრამ ამის შემდეგ არაფერი დაწეროთ.

ნაბიჯი 9. გაიმეორეთ იგივე ნაბიჯები შემდეგი ციფრის მოსაძებნად
ერთადერთი განსხვავება ისაა, რომ თქვენ უნდა დაამატოთ ათწილადის წერტილი ერთსა და იმავე ადგილას პასუხის ხაზში. ამის გაკეთების შემდეგ, თქვენ შეგიძლიათ მოძებნოთ დარჩენილი პასუხის ციფრები ზუსტად იმავე გზით.
-
მაგალითი:
ჩაწერეთ ახალი 0 ბოლო ხაზზე ისე, რომ ის გახდეს "60". ვინაიდან 60 გაყოფილი 12 -ზე არის ზუსტად 5, დაწერე
ნაბიჯი 5. როგორც ჩვენი პასუხის ხაზის ბოლო ციფრი. ნუ დაგავიწყდებათ, რომ ჩვენ ათწილადს ვდებთ პასუხების ხაზში. Ისე, 2, 5 არის საბოლოო პასუხი ჩვენს კითხვაზე.
Რჩევები
- თქვენ შეგიძლიათ ჩაწეროთ ეს დანარჩენად (ასე რომ პასუხი 3 1, 2 არის "2 დარჩენილი 6"). თუმცა, რადგან თქვენ ათწილადებთან მუშაობთ, თქვენს მასწავლებელს შეუძლია ელოდოს თქვენ, რომ იმუშაოთ პასუხის ათწილადზე.
- თუ სწორად მიჰყვებით გრძელი გაყოფის მეთოდს, თქვენ ყოველთვის გექნებათ ათწილადის წერტილი სწორ პოზიციაში, ან საერთოდ არ არის ათწილადი, თუ რიცხვი იყოფა გამყოფზე. ნუ ეცდებით ათწილადების გამოცნობას. ათწილადის ადგილი ხშირად განსხვავდება ათწილადისგან თქვენი საწყისი რიცხვისა.
- თუ გრძელი გაყოფის პრობლემა დიდხანს არ გაგრძელდება, შეგიძლიათ გაჩერდეთ და დამრგვალოთ უახლოეს რიცხვამდე. მაგალითად, 17 4, 2 - ის ამოსახსნელად, უბრალოდ დაითვალეთ 4.047 - მდე… და თქვენი პასუხი დამრგვალეთ „დაახლოებით 4.05“-ზე.
-
დაიმახსოვრე შენი გაყოფის პირობები:
- გასაყოფი რიცხვი არის გასაყოფი რიცხვი.
- გამყოფი არის რიცხვი, რომელიც გამოიყენება გაყოფისთვის.
- კოეფიციენტი არის მათემატიკის გაყოფის პრობლემის პასუხი.
- მთელი: იყოფა გამყოფი = კოეფიციენტი.
გაფრთხილება
გახსოვდეთ, რომ 30 12 გასცემს იგივე პასუხს, რაც 3 1, 2. ნუ ეცდებით თქვენი პასუხის „გასწორებას“ათწილადის უკან გადაადგილების შემდეგ
დაკავშირებული wiki სტატიები
- ჩვეულებრივი წილადების ათწილადებად გადაქცევა
- აკეთებს ხანგრძლივად განსაზღვრულ განყოფილებას
- წილადების გაყოფა წილადების მიხედვით
- შერეული წილადების გაყოფა






